图解线性代数.md

Generalized Linear Regression 通用线性回归

这一家族中的模型形式基本上都差不多，不同的就是因变量(Y)不同，如果是连续的，就是多重线性回归，如果是二项分布，就是logistic回归，如果是poisson分布，就是poisson回归，如果是负二项分布，就是负二项回归，等等。只要注意区分它们的因变量就可以了。logistic回归的因变量可以是二分类的(二项逻辑回归)，也可以是多分类的（多项逻辑回归或者softmax回归），但是二分类的更为常用，也更加容易解释。所以实际中最为常用的就是二分类的logistic回归。

逻辑回归(也是一种广义线性模型)

逻辑回归（非常详细）
机器学习实现与分析之四（广义线性模型）

逻辑回归——Logistic的起源
 Logistic回归的起源（上）
Logistic回归的起源（中）
Logistic回归的起源（下）

6.2 Logistic Regression and the Cross Entropy Cost - Logistic regression sklearn中代价函数

y属于0或1 (我们假设样本是服从伯努利分布(0-1分布)的，然后求得满足该分布的似然函数，最终求该似然函数的极大值)

6.3 Logistic Regression and the Softmax Cost-Logistic regression sklearn中代价函数

y属于-1或1

Logistic回归的损失函数:负对数似然,negative log likelihood(NLL), 负的log似然

Softmax回归是Logistic回归的多分类情况。
LogisticRegression 就是一个被logistic方程归一化后的线性回归。将预测的输出映射到0,1之间。

逻辑斯蒂回归模型的思想跟线性回归模型思想不一样，线性回归模型思想是最小化真实值与模型预测值的误差，而逻辑斯蒂回归模型思想就比较狠了，预测值预测对了损失函数就是0，错了损失就是无穷大，我个人的理解(一般采用的是-log(h(x)) 这是一个凸函数,刚好满足要求)

线性样条回归分析(linear spline regression)

Using splines in regression

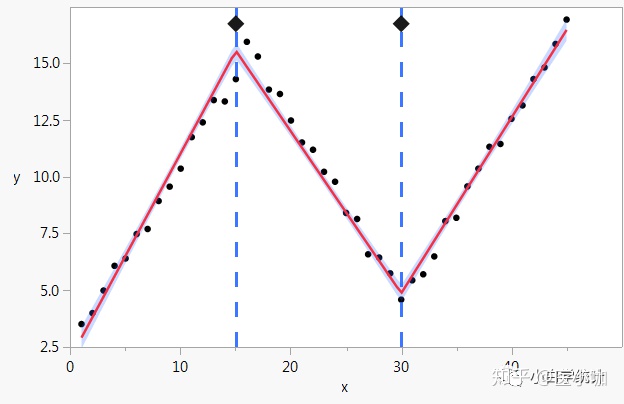
Least Angle Regression 最小角回归

Least Angle Regression

最小角回归法

由于LARS的迭代方向是根据目标的残差而定，所以该算法对样本的噪声极为敏感。

图解机器学习的数学直觉：线性代数，微积分，PCA

https://www.bilibili.com/video/BV1iW411T781

如何理解主元分析（PCA）？

https://matongxue.blog.csdn.net/article/details/82254488
PCA的数学原理

通俗易懂的PCA原理及代码实现(超详细推导)

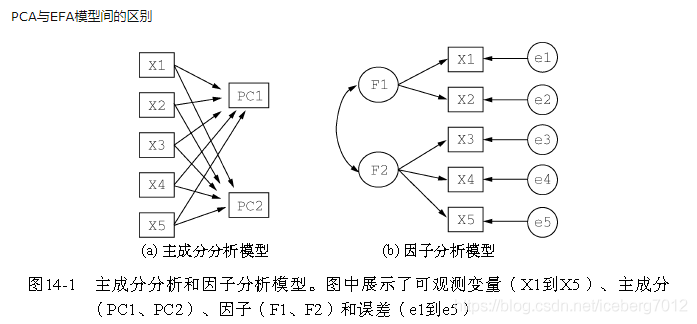
主成分分析，是分析维度属性的主要成分表示。
因子分析，是分析属性们的公共部分的表示。
二者均应用于高斯分布的数据，非高斯分布的数据采用独立成分分析ICA算法
如果做分类问题之前用PCA降维，效果可能会更差

因子分析Factor Analysis(FA)

可以应用于高维数据维度m>>p

每个变量都可以表示成公共因子的线性函数与特殊因子之和

\[X_i = a_{i1}F_1 + a_{i2}F_2 +...++ a_{im}F_m + \epsilon_i ,(i=1,2,...,p) \]

式中的F1，F2，…，Fm称为公共因子，εi称为Xi的特殊因子。该模型可用矩阵表示为：X = AF+ε
X 表示原始数据，矩阵A称为因子载荷矩阵,F表示公共因子， ε是特殊因子
aij称为因子“载荷”，是第i个变量在第j个因子上的负荷，如果把变量Xi看成m维空间中的一个点，则aij表示它在坐标轴Fj上的投影。
$X = [X_1,X_2...X_p]^T$

$A= \begin{bmatrix}
a_{11} & a_{12} & ... & a_{1m} \\
a_{21} & a_{22} & ... & a_{2m} \\
... & ... & ... & ... \\
a_{p1} & a_{p2} & ... & a_{pm} \\
\end{bmatrix}$

$F = [F_1,F_2...F_m]^T$

$\epsilon = [\epsilon_1,\epsilon_2...\epsilon_p]^T$

m<=p

Independent component analysis(ICA)，独立成分分析

Independent component analysis

X=AS
Y=WX=WAS ， A = inv(W)
ICA(Independent Component Correlation Algorithm)是一种函数，X为n维观测信号矢量，S为独立的m（m<=n)维未知源信号矢量，矩阵A被称为混合矩阵。
ICA的目的就是寻找解混矩阵W（A的逆矩阵），然后对X进行线性变换，得到输出向量Y。

ICA是找出构成信号的相互独立部分(不需要正交)，对应高阶统计量分析。ICA理论认为用来观测的混合数据阵X是由独立元S经过A线性加权获得。
ICA理论的目标就是通过X求得一个分离矩阵W，使得W作用在X上所获得的信号Y是独立源S的最优逼近，

独立成分分析 (ICA) 应用参考(Origin来做ICA分析)

独立成分分析 - 讲解的原理

Independent Component Analysis (ICA)

SVM 支持向量机算法-原理篇

https://www.cnblogs.com/codeshell/p/14301569.html

[胡浩基教授SVM](files/胡浩基-机器学习笔记/1. 支持向量机的理论推导.pdf)

支持向量机-完整版

李宏毅深度学习笔记-SVM支持向量机
深度学习和SVM的区别:
深度学习的隐藏层可以看成是特征转换，输出层可以看成是线性分类器。

SVM也是做类似的事情，先用一个核函数，把特征转换到高维空间上，再在高维空间使用线性分类器，线性分类器的损失函数一般使用hinge loss。

奇异值分解SVD

如何通俗地理解奇异值
 奇异值的物理意义是什么？
Singular value decomposition
We Recommend a Singular Value Decomposition

降维

白板推导系列(系列五) 降维1-背景视频

13分的时候就知道为什么在边缘了

白板推导系列(系列五) 降维1-背景文字

线性判别分析LDA

线性判别分析LDA原理总结
 LDA
Linear Discriminant Analysis (LDA)

线性判别分析（Linear Discriminant Analysis）

线性判别分析（LDA）假设$f_k(x)$是均值不同，方差相同的高斯分布
二次判别分析（QDA）假设$f_k(x)$是均值不同，方差也不同的高斯分布
高斯混合模型（GMM）假设$f_k(x)$是不同的高斯分布的组合
很多非参数方法假设$f_k(x)$是参数的密度函数，比如直方图
朴素贝叶斯假设$f_k(x)$是$C_k$边缘密度函数，即类别之间是独立同分布的
如果在 QDA 模型中假设协方差矩阵是对角矩阵，则假设输入在每个类中条件独立，并且生成的分类器等效于高斯朴素贝叶斯分类器naive_bayes.GaussianNB

机器学习-白板推导系列(四)-线性分类（Linear Classification）+ 推荐
 线性判别分析（Linear Discriminant Analysis）（一）+ 推荐

为什么叫线性判别分析和二次判别分析

The Elements of Statistical Learning 128页的(4.10)和129页的(4.12)

R. O. Duda, P. E. Hart, D. G. Stork. Pattern Classification (Second Edition)59页2.6.2 Case 2: Σi = Σ (大概的意思是展开后二次项与i无关，可以丢掉)

LDA-math:神奇的Gamma函数(1)
LDA-math-神奇的Gamma函数(2)
LDA-math-神奇的Gamma函数(3)
LDA-math-认识Beta/Dirichlet分布(1)
LDA-math-认识Beta/Dirichlet分布(2)
LDA-math-认识Beta/Dirichlet分布(3)

高斯视角

高斯判别分析（Gaussian discriminant analysis model, GDA）- 生成学习算法

GDA（高斯判别分析）是 LDA（线性判别分析）和 QDA（二次判别分析）的通用术语，其中给定类别的每个观察的似然概率，即 P(x|y) 可以通过多变量建模高斯分布。

LDA - QDA

Linear and Quadratic Discriminant Analysis

机器学习实现与分析之五（高斯判别分析）

【机器学习】高斯判别分析

综合

难懂的数学】傅里叶、拉普拉斯、卷积、欧拉方程、梯度散度、拉格朗日方程、奈奎斯特采样、虚数等抽象难懂数学一网打尽

机器学习算法的动画可视化

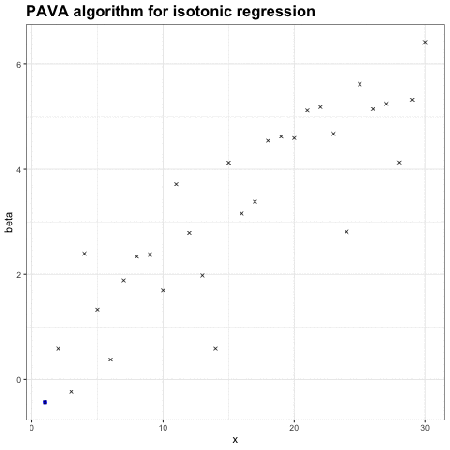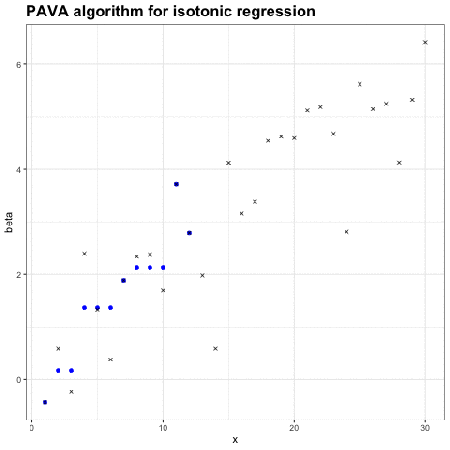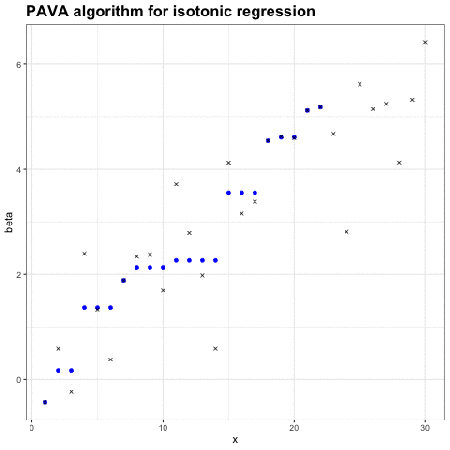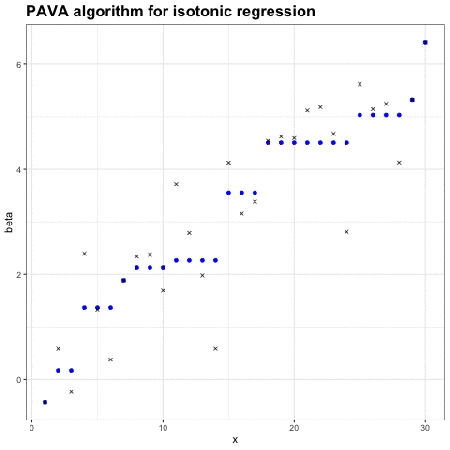
保序回归：单调不减

Isotonic Regression

K-means聚类

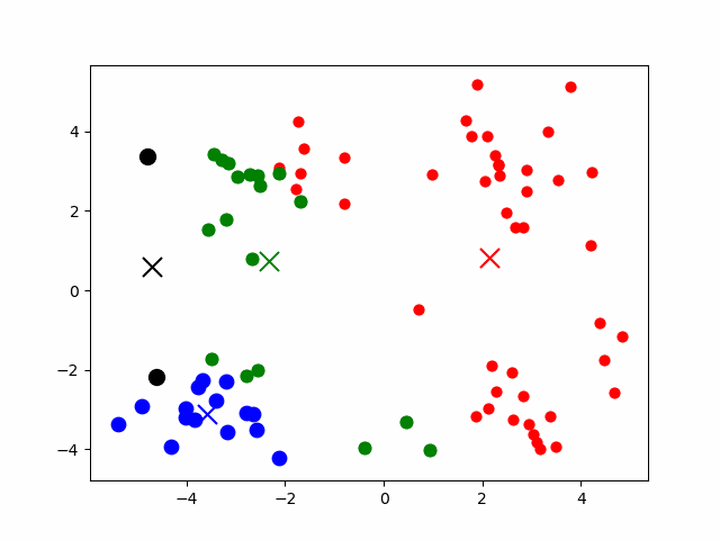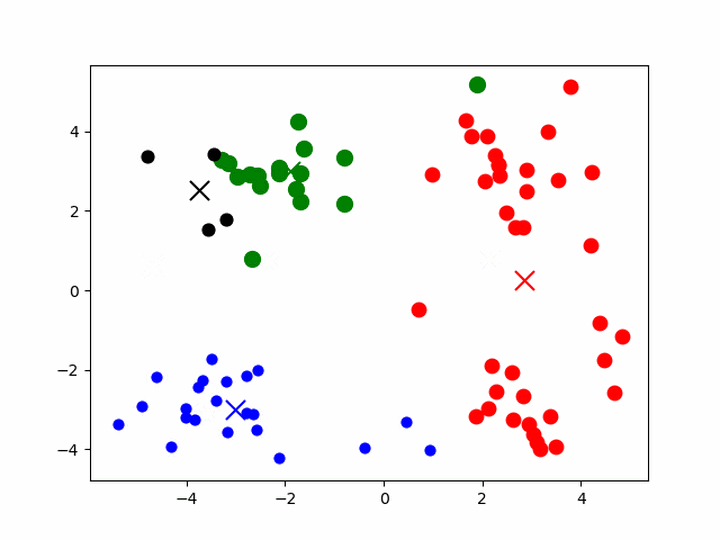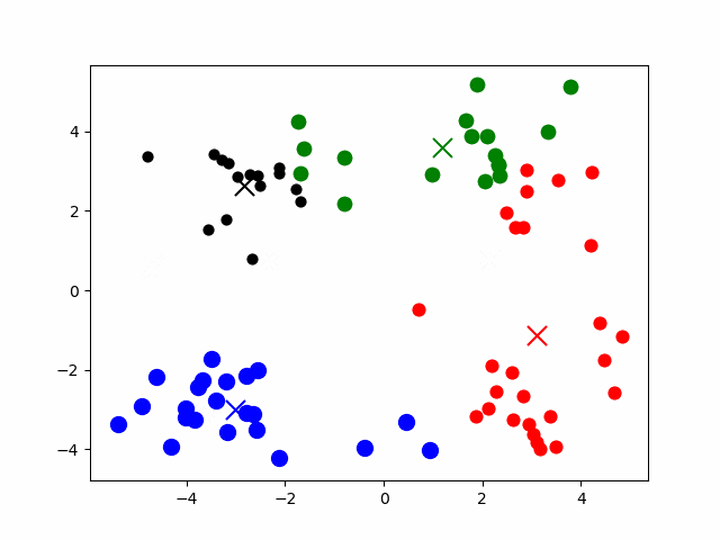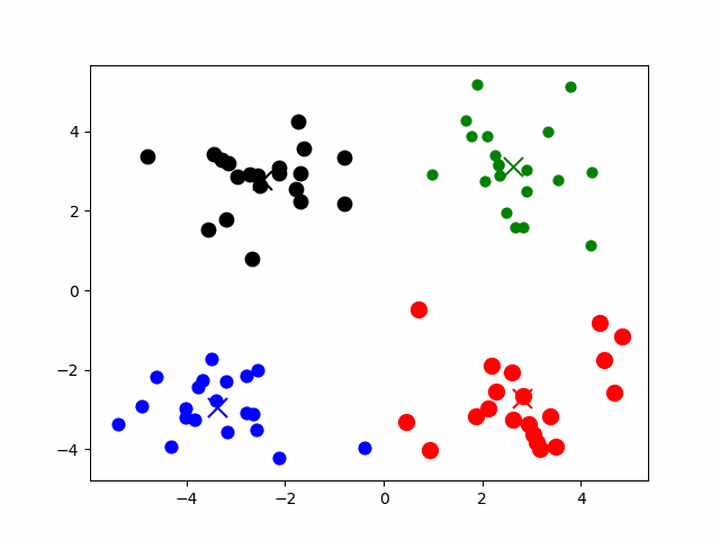
给定一组样本，确定k值，即类别数目
随机初始化k个聚类的中心（质心，下称中心）
计算每个样本与每一个中心的相似的程度——距离
考察每个样本，离哪一个中心更近，就将该样本分为哪一类
所有样本划分完毕后，根据已分好的数据，重新计算聚类的中心
重复3、4、5，直到中心不变或者变化很小

可视化k-means
可视化Visualizing DBSCAN Clustering

scikit-learn除了标准的变分推断EM算法外，还实现了另一种在线变分推断EM算法，它在原理篇里的变分推断EM算法的基础上，为了避免文档内容太多太大而超过内存大小，而提供了分步训练(partial_fit函数)，即一次训练一小批样本文档，逐步更新模型，最终得到所有文档LDA模型的方法。这个改进算法我们没有讲，具体论文在这
Online Learning for Latent Dirichlet Allocation M. Hoffman, D. Blei, F. Bach, 2010

Latent Dirichlet allocation

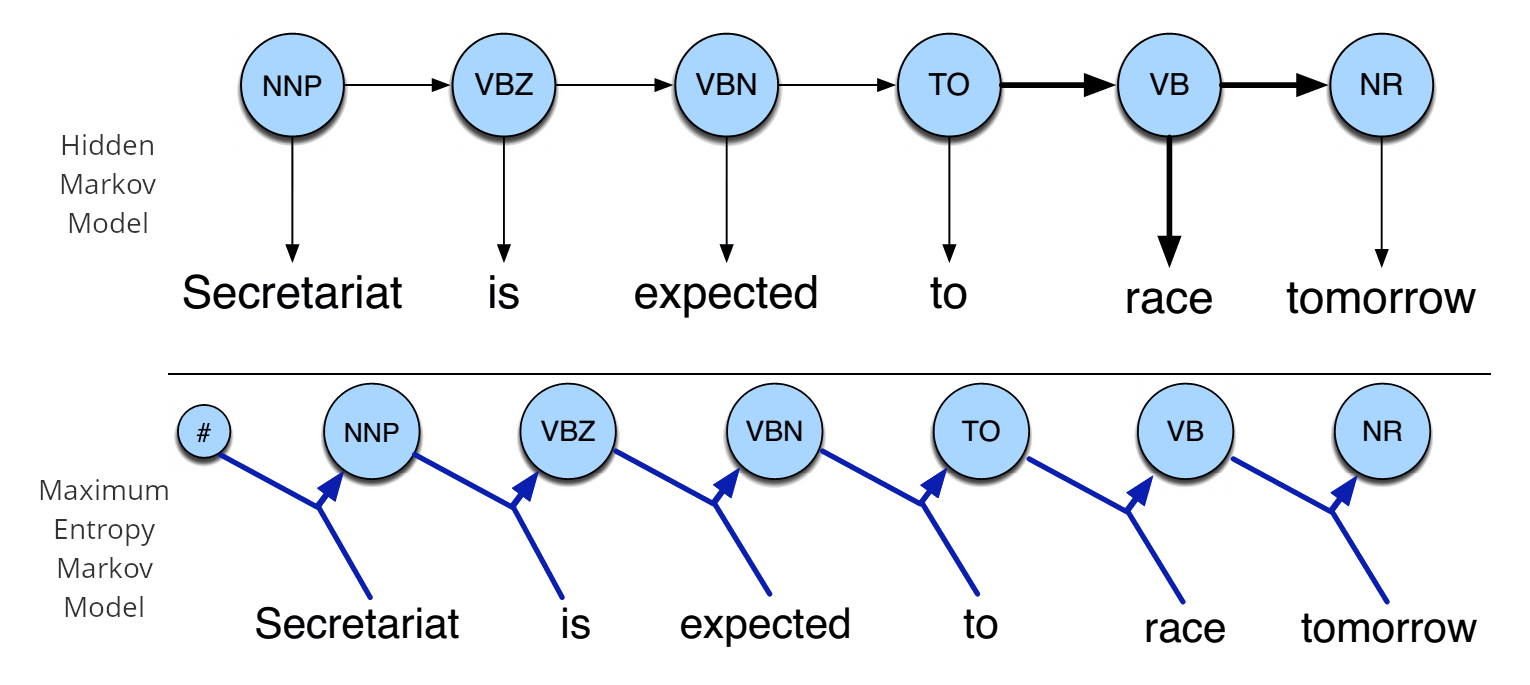
Hidden Markov Models

Hidden Markov model

Hidden Markov Models and Gaussian Mixture Models

hmmlearn

Maximum Entropy Markov Model

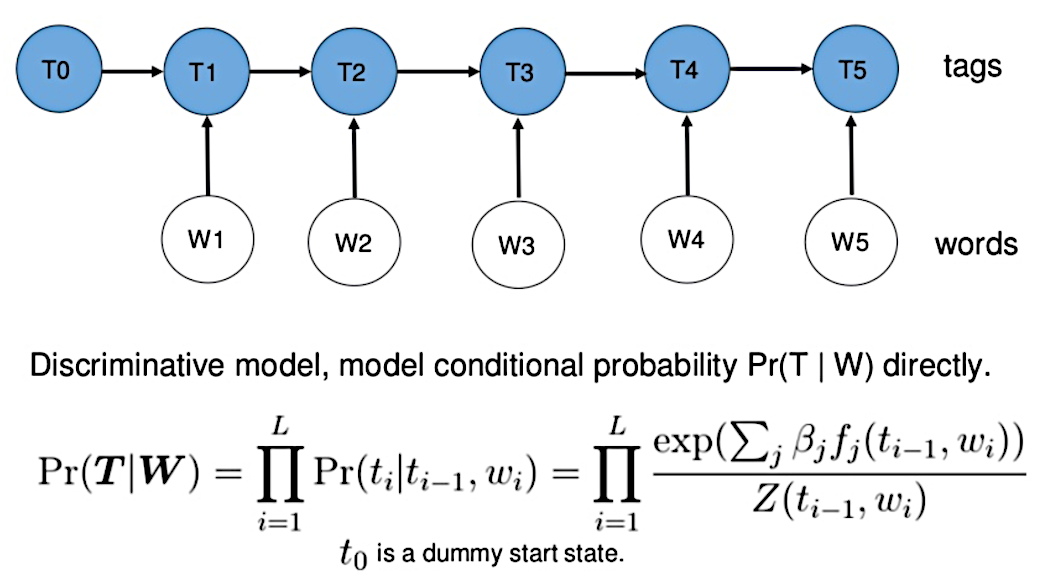
Maximum-entropy Markov model

Conditional random field

Conditional random field
Conditional Random Fields

隐马尔可夫模型（Hidden Markov Model，HMM），最大熵马尔可夫模型（Maximum Entropy Markov Model，MEMM）以及条件随机场（Conditional Random Field，CRF）是序列标注中最常用也是最基本的三个模型。
HMM、CRF、MEMM区别

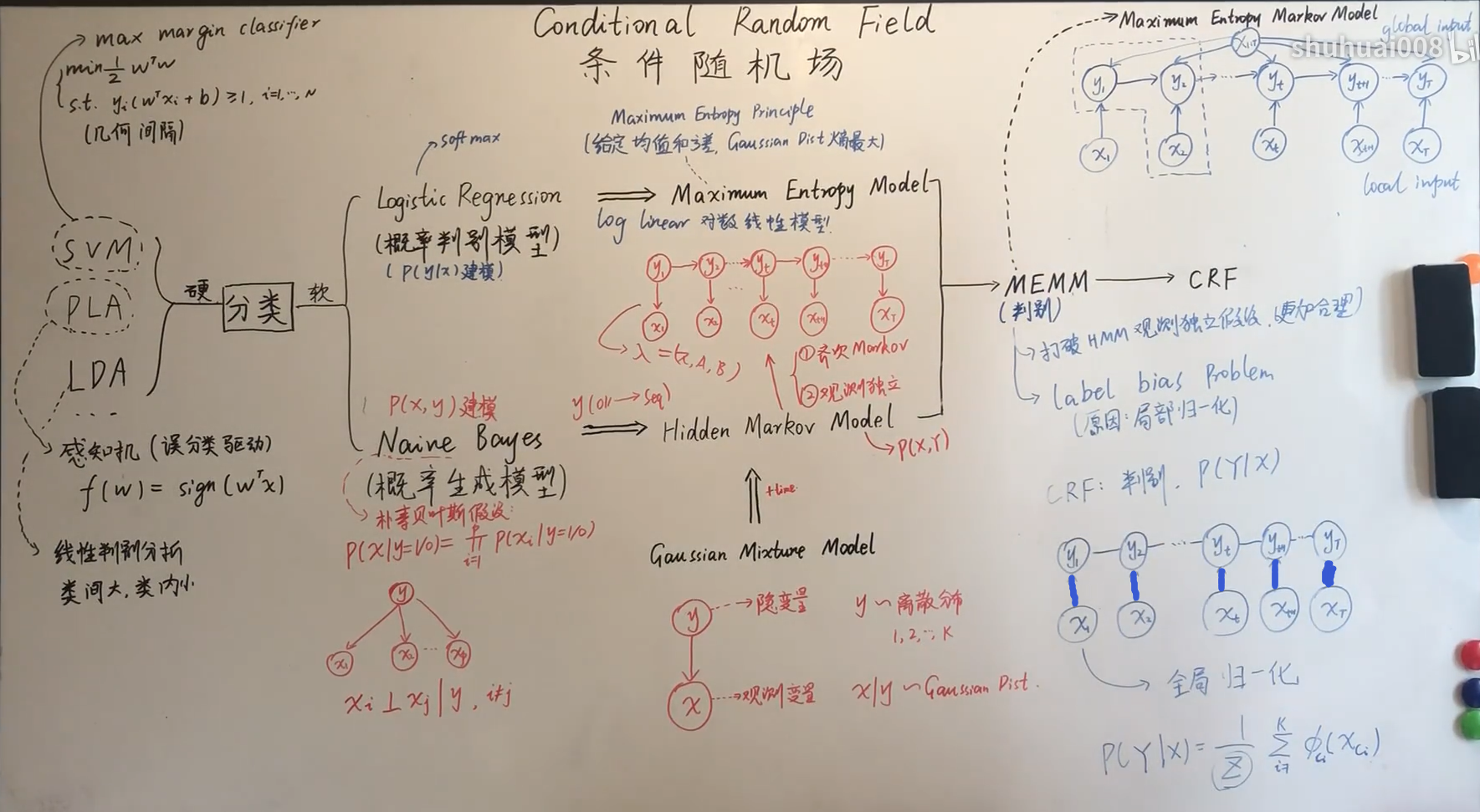
HMM -> MEMM： HMM模型中存在两个假设：一是输出观察值之间严格独立，二是状态的转移过程中当前状态只与前一状态有关。但实际上序列标注问题不仅和单个词相关，而且和观察序列的长度，单词的上下文，等等相关。MEMM解决了HMM输出独立性假设的问题。因为HMM只限定在了观测与状态之间的依赖，而MEMM引入自定义特征函数，不仅可以表达观测之间的依赖，还可表示当前观测与前后多个状态之间的复杂依赖。

MEMM -> CRF:CRF不仅解决了HMM输出独立性假设的问题，还解决了MEMM的标注偏置问题，MEMM容易陷入局部最优是因为只在局部做归一化，而CRF统计了全局概率，在做归一化时考虑了数据在全局的分布，而不是仅仅在局部归一化，这样就解决了MEMM中的标记偏置的问题。使得序列标注的解码变得最优解。

HMM、MEMM属于有向图，所以考虑了x与y的影响，但没讲x当做整体考虑进去（这点问题应该只有HMM）。CRF属于无向图，没有这种依赖性，克服此问题。

Hidden Markov Model and Naive Bayes relationship
Maximum Entropy Markov Models and Logistic Regression
Conditional Random Fields for Sequence Prediction

Random projection

Johnson–Lindenstrauss lemma
Random projection

Gaussian random projection & Sparse random projection 区别在于生成random matrix的方式不同（Sparse指的也是random matrix是Sparse的），而random matrix用于投影的，维度是降维后的维度*降维前的维度（Sparse：transformer.components_.toarray()；Gaussian：transformer.components_）

Table of Contents