Table of Contents

• 径向基函数（Radical Basis Function,RBF）
  • RBF网络模型
  • RBF网络学习算法
  • 径向基函数
  • 参考

径向基函数（Radical Basis Function,RBF）

1985年，Powell提出了多变量插值的径向基函数（Radical Basis Function,RBF）方法。1988年，Moody和Darken提出了一种神经网络结构，即RBF神经网络，属于前向神经网络类型，它能够以任意精度逼近任意连续函数，特别适合于解决分类问题。

RBF网络模型

径向基神经网络的激活函数采用径向基函数，通常定义为空间任一点到某一中心之间欧氏距离的单调函数。径向基神经网络的激活函数是以输入向量和权值向量之间的距||dist||为自变量的。径向神经网络的激活函数一般表达式为 \(\mathcal{R}\)(||dist||) = \(e^{-||dist||^2}\)

RBF网络学习算法

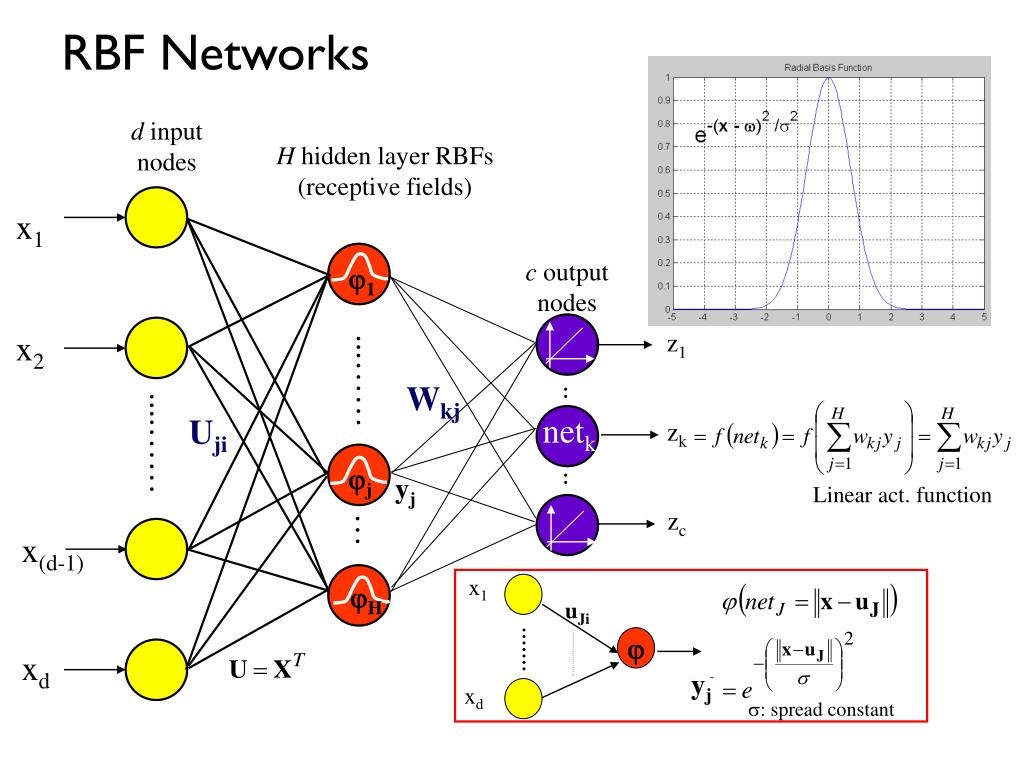
径向基函数

• Gauss（高斯）函数
  \({\phi}(r) = exp(-\frac{r^2}{2{\sigma}^2})\)
  

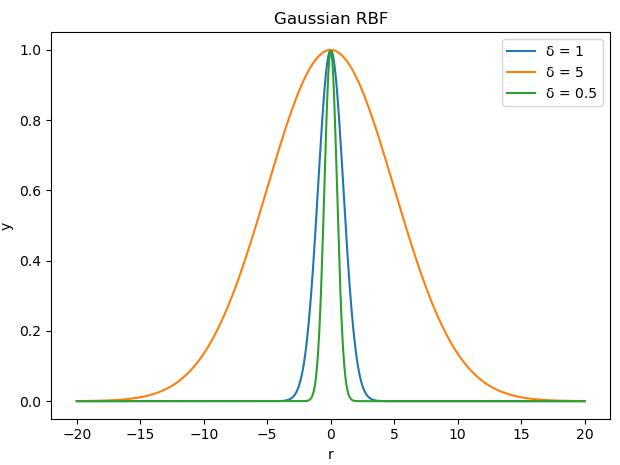
import numpy as np
import matplotlib.pyplot as plt

r = np.linspace(-20, 20, 500)
plt.xlabel("r")
plt.ylabel("y")
plt.title("Gaussian RBF")
for delta in [1, 5, 0.5]:
    y = np.exp(-(r ** 2 / (2 * delta ** 2)))
    plt.plot(r, y, label="δ = " + str(delta))

plt.legend()  # 将plot标签里面的图注印上去
plt.show()

• Reflected Sigmoidal（反常S型）函数
  \({\phi}(r) = \frac{1}{1+exp(\frac{r^2}{\sigma}^2)}\)

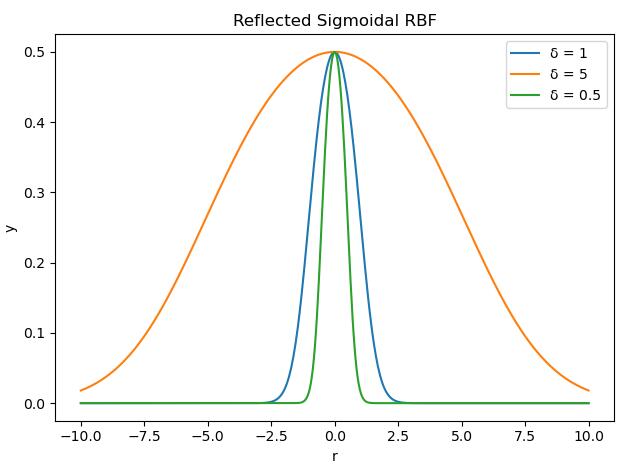
import numpy as np
import matplotlib.pyplot as plt

r = np.linspace(-20, 20, 500)
plt.xlabel("r")
plt.ylabel("y")
plt.title("Reflected Sigmoidal RBF")
for delta in [1, 5, 0.5]:
    y = 1 / (1 + np.exp(r ** 2 / delta ** 2))
    plt.plot(r, y, label="δ = " + str(delta))

plt.legend()  # 将plot标签里面的图注印上去
plt.show()

sympy绘图

from sympy.plotting import plot
from sympy import symbols
from sympy.functions import exp

r = symbols('r')
p = []
for delta in [1, 5, 0.5]:
    y = 1 / (1 + exp(r ** 2 / delta ** 2))
    p.append((y, (r, -10, 10)))
p2 = plot(*p)

• Inverse multiquadrics（拟多二次）函数
  \({\phi}(r) = \frac{1}{\sqrt{r^2+{\sigma}^2}}\)

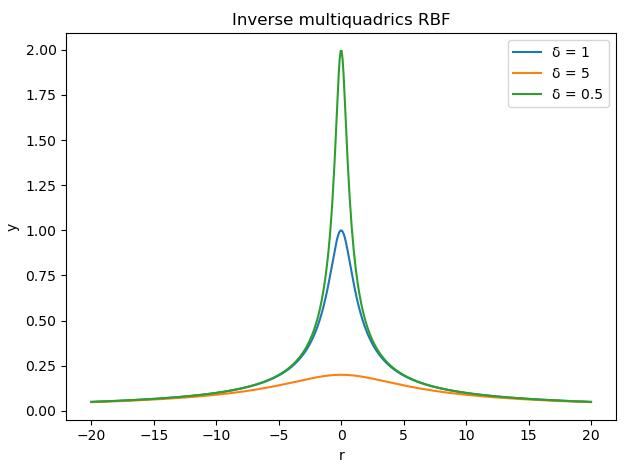
import numpy as np
import matplotlib.pyplot as plt

r = np.linspace(-20, 20, 500)
plt.xlabel("r")
plt.ylabel("y")
plt.title("Inverse multiquadrics RBF")
for delta in [1, 5, 0.5]:
    y = 1 / (np.sqrt(r ** 2 + delta ** 2))
    plt.plot(r, y, label="δ = " + str(delta))

plt.legend()  # 将plot标签里面的图注印上去
plt.show()

参考

径向基神经网络
Radial basis function
Radial basis function kernel