Table of Contents
[TOC]
第 13 章 无监督学习概论
基本问题:
聚类(clustering)是将样本集合中相似的样本归到相同的类,相似的定义一般用距离度量。
如果一个样本只能属于一个类,则称为硬聚类(hard clustering),如k-means;如果一个样本可以属于多个类,每一个样本以概率属于每一个类\(\sum_{i=1}^N p(z_i|x_i) =1\),则称为软聚类(soft clustering),如GMM。
聚类主要用于数据分析,也可用于监督学习的前处理。聚类可以帮助发现数据中的统计规律。
降维(dimensionality reduction)是将样本集合中的样本(实例)从高维空间转换到低维空间。
高维空间通常是高维的欧氏空间,而低维空间是低维的欧氏空间或流形(manifold)。低维空间是从数据中自动发现的。降维有线性降维和非线性降维,降维方法有主成分分析。
降维的好处有:节省存储空间、加速计算、解决维度灾难(前面章节有讲到)等
降维主要用于数据分析,也可用于监督学习的前处理。降维可以帮助发现高维数据中的统计规律。
概率模型估计(probability model estimation),简称概率估计,假设训练数据由一个概率模型生成,由训练数据学习概率模型的结构和参数。
概率模型的结构类型或者概率模型的集合事先给定,而模型的具体结构与参数从数据中自动学习。假设数据由GMM生成(已知结构),学习的目标是估计这个模型的参数。
概率模型包括混合模型、概率图模型等。概率图模型又包括有向图模型和无向图模型(前面章节有讲到)。
无监督学习方法
-
聚类
- 硬聚类:
- k-means
- 软聚类:
- GMM
- 硬聚类:
-
降维
- 线性:
- 主成分分析
- 非线性:
- 流形学习
- 线性:
-
话题分析
话题分析是文本分析的一种技术。给定一个文本集合,话题分析旨在发现文本集合中每个文本的话题,而话题由单词的集合表示。话题分析方法有:- 潜在语义分析
- 概率潜在语义分析
- 潜在狄利克雷分配
-
图分析
图分析 的目的是 发掘隐藏在图中的统计规律或潜在结构;- 链接分析 是图分析的一种,主要是发现 有向图中的重要结点,包括 PageRank 算法
- PageRank 算法最初是为互联网搜索而提出。将互联网看作是一个巨大的有向图,网页是结点,网页的超链接是有向边。PageRank 算法可以算出网页的 PageRank 值,表示其重要度,在搜索引擎的排序中网页的重要度起着重要作用
同监督学习一样,无监督学习也有三要素:模型、策略、算法
模型 就是函数\(z=g_\theta(x)\),条件概率分布\(P_\theta(z |x)\),或\(P_\theta(x|z)\),在聚类、降维、概率模型估计中拥有不同的形式
- 聚类 中模型的输出是 类别
- 降维 中模型的输出是 低维向量
- 概率模型估计 中的模型可以是混合概率模型,也可以是有向概率图模型和无向概率图模型
策略 在不同的问题中有不同的形式,但都可以表示为目标函数的优化
- 聚类 中样本与所属类别中心距离的最小化
- 降维 中样本从高维空间转换到低维空间过程中信息损失的最小化
- 概率模型估计 中模型生成数据概率的最大化
算法 通常是迭代算法,通过迭代达到目标函数的最优化,比如,梯度下降法。
- 层次聚类法、k均值聚类 是硬聚类方法
- 高斯混合模型 EM算法是软聚类方法
- 主成分分析、潜在语义分析 是降维方法
- 概率潜在语义分析、潜在狄利克雷分配 是概率模型估计方法
参考文献
[13-1] Hastie T, Tibshirani R, Friedman J. The elements of statistical learning:data mining, inference, and prediction. Springer. 2001.
[13-2] Bishop M. Pattern Recognition and Machine Learning. Springer, 2006.
[13-3] Koller D, Friedman N. Probabilistic graphical models: principles and techniques. Cambridge, MA: MIT Press, 2009.
[13-4] Goodfellow I,Bengio Y,Courville A. Deep learning. Cambridge, MA: MIT Press, 2016.
[13-5] Michelle T M. Machine Learning. McGraw-Hill Companies, Inc. 1997.(中译本:机器学习。北京:机械工业出版社,2003.)
[13-6] Barber D. Bayesian reasoning and machine learning, Cambridge, UK:Cambridge University Press, 2012.
[13-7] 周志华. 机器学习. 北京:清华大学出版社,2017.
第 14 章 聚类方法
聚类分析(Cluster analysis or clustering)是针对给定的样本,根据它们特征点的相似度(距离),将其归并到若干个类(簇)中的分析问题。聚类分析本身不是一种特定的算法,而是要解决的一般任务。
算法分类
Hard clustering
Soft clustering (also: fuzzy clustering)
Connectivity models:如 hierarchical clustering 基于距离连通性(based on distance connectivity)
Centroid models:如 k-means
Distribution models:如GMM
Density models:如 DBSCAN and OPTICS
Subspace models:如 biclustering
Group models:如
Graph-based models:如
Signed graph models:如
Neural models:如
聚类分析算法(Cluster analysis algorithms):sklearn中的聚类算法和介绍
基于连接的聚类(层次聚类) Connectivity-based clustering(Hierarchical clustering):
层次聚类有聚合Agglomerative(自下而上"bottom-up")和分裂 Divisive(自上而下"top-down")两种方法。
- sklearn.cluster.AgglomerativeClustering
从下而上地把小的cluster合并聚集,开始时将每个样本各自分到一个cluster,之后将距离最短的两个cluster合并成一个新的cluster,重复此步骤直到满足停止条件;
书中提到三个要素:
- 距离度量或相似度
- 合并规则(cluster间的距离规则,cluster间的距离可以是最短、最长、中心距离、平均距离等)
- 停止条件(达到k值,也就是cluster的个数达到阈值;cluster的直径达到阈值;)
- DIANA (DIvisive ANAlysis Clustering) algorithm
开始将所有样本归为一个cluster,之后将距离最远的两个样本分到两个新的cluster,重复此步骤直到满足停止条件;
基于质心的聚类 Centroid-based clustering:
-
K均值聚类(k-means clustering),sklearn.cluster.KMeans
KMeans 可以看作是高斯混合模型的一个特例,每个分量的协方差相等。 -
均值移位聚类(Mean shift clustering) ,sklearn.cluster.MeanShift
Mean shift clustering using a flat kernel. based on kernel density estimation.
sklearn中有说是centroid-based。维基百科把它放在基于密度的聚类中(核密度估计)。 -
亲和力传播(Affinity Propagation (AP)),sklearn.cluster.AffinityPropagation
基于数据点之间“消息传递”的概念。based on the concept of "message passing" between data points.
基于分布的聚类 Distribution-based clustering:
- 高斯混合模型聚类(Gaussian mixture model),sklearn.mixture
基于密度的聚类 Density-based clustering:
- 基于密度的带噪声应用空间聚类(Density-Based Spatial Clustering of Applications with Noise (DBSCAN)),sklearn.cluster.DBSCAN
- 对象排序识别聚类结构(Ordering Points To Identify the Clustering Structure (OPTICS)) ,sklearn.cluster.OPTICS
基于网格的聚类 Grid-based clustering:
其它聚类:
- 谱聚类(Spectral clustering),sklearn.cluster.SpectralClustering
- 双聚类(biclustering),谱双聚类sklearn.cluster.SpectralBiclustering,谱协同聚类sklearn.cluster.SpectralCoclustering
高效聚类:
- 使用层次结构平衡迭代减少和聚类 (Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH)) ,sklearn.cluster.Birch
它是一种高效内存的在线学习算法,可作为MiniBatchKMeans的替代方案。它构造了一个树状数据结构,其中集群中心被从叶子中读取。这些可以是最终的聚类中心,也可以作为输入提供给其他聚类算法,如 AgglomerativeClustering。
高维数据的聚类(Clustering high-dimensional data):
子空间聚类Subspace clustering
投影聚类Projected clustering
基于投影的聚类Projection-based clustering
混合方法Hybrid approaches
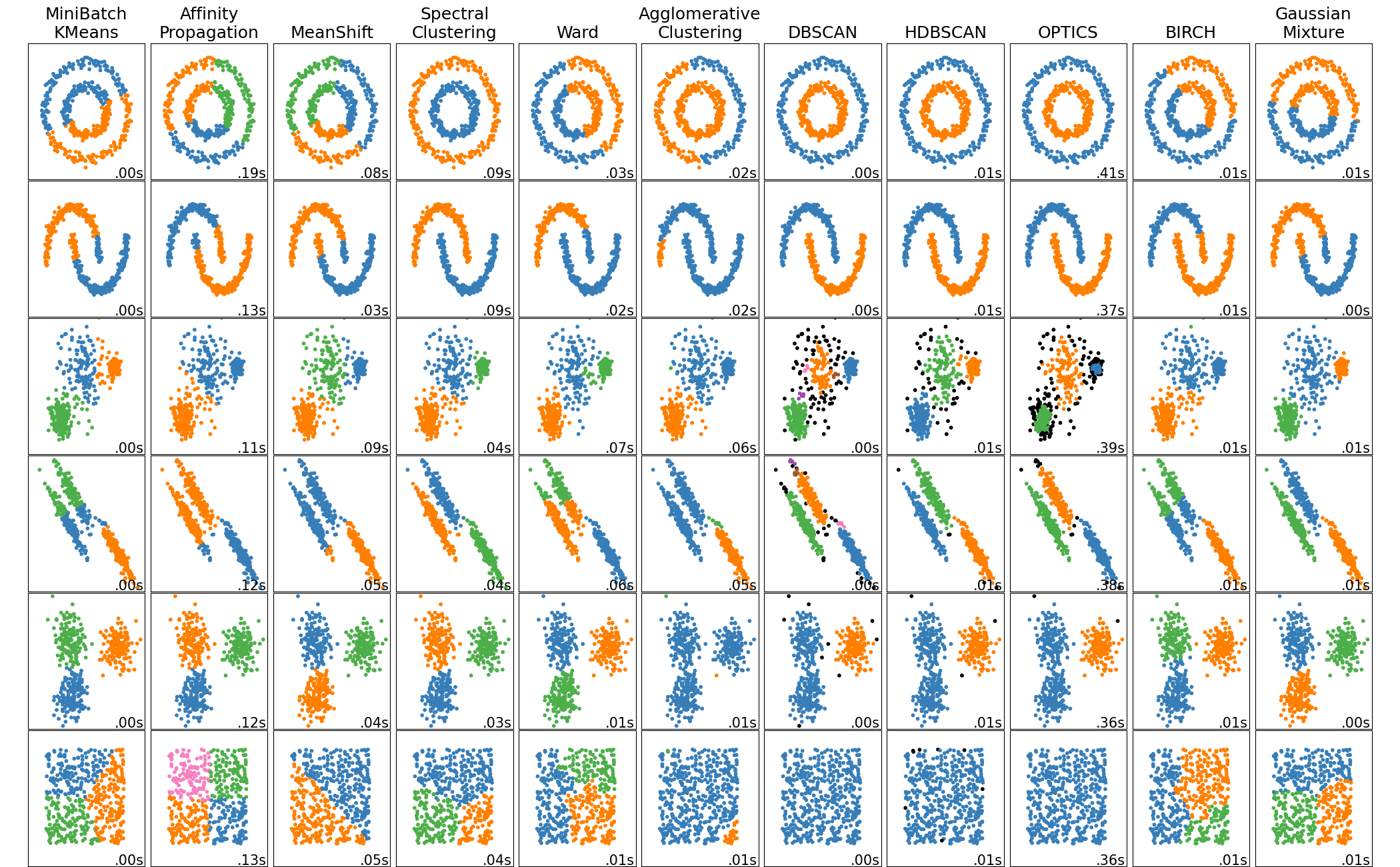
算法评估Evaluation
聚类结果的评估与聚类本身一样困难(并不像计算错误数量或监督分类算法的精度和召回率那么简单)。一般分为Internal evaluation和External evaluation,当两种评估效果都不好时就需要human evaluation。
先作一些定义:
数据集\(D=\{x_1,x_2,...,x_i,...,x_j,...,x_n\}\)
设\(T\)为给定的正数,若集合\(C_p\)中任意两个样本间的距离\(dist(x_i,x_j) \leq T\),则称\(C_p\)为一个类或簇(cluster)
\(C = \{C_1,C_2,...,C_k\}\)表示(预测的)类或簇(cluster)
\(C^* = \{C_1^*,C_2^*,...,C_s^*\}\)表示参考模型的类或簇(cluster)
\(\lambda\)表示簇\(C\)的标记(预测)向量,如:\(\lambda = [0,1,...,k],\lambda^* = [0,1,...,s]\),长度为样本数量\(n\)
\(\lambda_i\)为样本\(x_i\)的预测或标记值
\(a = TP, TP=\{(x_i,x_j)\mid\lambda_i = \lambda_j, \lambda_i^* = \lambda_j^* ,i \lt j\}\) ,表示“样本对”在\(C\)中属于相同的簇且在\(C^*\)中也属于相同的簇的数量(true positive)
\(b = TN, TN=\{(x_i,x_j)\mid\lambda_i = \lambda_j, \lambda_i^* \neq \lambda_j^* ,i \lt j\}\) ,表示“样本对”在\(C\)中属于相同的簇且在\(C^*\)中也属于不同的簇的数量(true negative)
\(c = FP, FP=\{(x_i,x_j)\mid\lambda_i \neq \lambda_j, \lambda_i^* = \lambda_j^* ,i\lt j\}\) ,表示“样本对”在\(C\)中属于不同的簇且在\(C^*\)中也属于相同的簇的数量(false positive)
\(d = FN, FN=\{(x_i,x_j) \mid \lambda_i \neq \lambda_j, \lambda_i^* \neq \lambda_j^* ,i\lt j\}\) ,表示“样本对”在\(C\)中属于不同的簇且在\(C^*\)中也属于不同的簇的数量(false negative)
注意:labels_pred = [0, 0, 1, 1] 与 labels_true = [0, 0, 1, 1] 以及 labels_pred = [0, 0, 1, 1] 与 labels_true = [1, 1, 0, 0] 是没有区别的,他们都正确的聚类了。
样本对的数量为\(C_n^2 = \binom{n}{2} =n(n-1)/2 = a+b+c+d\),这里的\(C\)是排列组合的意思
\(d_{ij} = dist(x_i,x_j)\)表示样本\(x_i,x_j\)之间的距离
\(n_p = |C_p|\)表示簇\(C_p\)中的样本数量,
\(\bar{x}_p = \frac{1}{n_p}\sum_{x_i \in C_p}x_i\)分别表示簇\(C_p\)的质心(中心、均值、中心点、centroid)
\(diam(C_p) = \max \{dist(x_i,x_j) \mid x_i,x_j \in C_p\}\)表示簇的直径diam或者簇类样本间的最远距离
\(avg(C_p) = \frac{2}{n_p(n_p-1)} \sum_{1\leq i \lt j\leq n_p }dist(x_i,x_j)\)表示簇类样本间的平均距离
\(A_{C_p} = \sum_{x_i \in C_p} (x_i-\bar{x}_p)(x_i-\bar{x}_p)^T\)表示簇类样本散布矩阵(scatter matrix)
\(S_{C_p} = \frac{1}{n_p-1}A_{C_p}\)表示簇类样本协方差矩阵(covariance matrix)
两个簇之间的距离主要有以下表示方法:
\(d_{min}(C_p,C_q) = \min\{dist(x_i,x_j) \mid x_i \in C_p,x_j \in C_q\}\)表示两个簇间的最短距离
\(d_{max}(C_p,C_q) = \max\{dist(x_i,x_j) \mid x_i \in C_p,x_j \in C_q\}\)表示两个簇间的最长距离
\(d_{cen}(C_p,C_q) = dist(\bar{x}_p,\bar{x}_q)\)表示两个簇中心间的距离
\(d_{mean}(C_p,C_q) = \frac{1}{n_p n_q}\sum_{x_i \in G_p}\sum_{x_j \in G_q} dist(x_i,x_j)\)表示两个簇 任意两个样本之间距离的平均值 为两个簇的距离
聚类标准(Clustering criteria):簇内相似度(intra-cluster similarity)高,簇间相似度(inter-cluster similarity)低
确定数据集中的簇数(Determining the number of clusters in a data set),也就是K值的选取。
对于某类聚类算法(特别是k-means, k-medoids),有一个通常称为k的参数指定要检测的聚类数。其他算法如DBSCAN和OPTICS 算法不需要指定该参数;层次聚类完全避免了这个问题。
簇数是数据集中重要的概括统计量。经验值:\(k \thickapprox \sqrt{n/2}\)
-
肘方法(Elbow method)
给定k>0,使用像K-均值这样的算法对数据集聚类,并计算簇内方差和var(k)。然后,绘制var关于k的曲线。曲线的第一个(或最显著的)拐点暗示“正确的”簇数。 -
X-means clustering
-
Information criterion approach
-
Information–theoretic approach
-
轮廓系数(Silhouette method)
-
Cross-validation
-
Finding number of clusters in text databases
-
Analyzing the kernel matrix
Internal evaluation:
无监督的方法,无需基准数据。类内聚集程度和类间离散程度。簇内相似度(intra-cluster similarity)高,簇间相似度(inter-cluster similarity)低。
- DB指数(Davies-Bouldin Index, DBI)
\[DBI={\frac {1}{k}}\sum _{i=1}^{k}\max _{j\neq i}\left({\frac {avg(C_i)+avg(C_j)}{d_{cen}(C_{i},C_{j})}}\right)\]
DBI值越小越好,也就是\(avg(C_i)\)越小,簇内相似度越高;\(d_{cen}(C_{i},C_{j})\)越大,簇间相似度越低。
metrics.davies_bouldin_score
- 轮廓系数(Silhouette coefficient)
\[{\displaystyle a(x_i)={\frac {1}{|C_{p}|-1}}\sum _{x_i,x_j\in C_{p},i\neq j}dist(x_i,x_j)}\]
\(a(x_i)\)表示每个样本点与簇\(C_{p}\)内其它样本点的平均距离(值越小表示分配的越好)
\[{\displaystyle b(x_i)=\min _{q\neq p}{\frac {1}{|C_{q}|}}\sum _{x_i\in C_{p},x_j\in C_{q}}dist(x_i,x_j) }\]
平均相异度:簇\(C_{p}\)中样本点\(x_i\)到其它簇\(C_{q}\)中所有的样本点的平均距离(越大说明簇间相似度越低)
\(b(x_i)\)表示最小平均相异度。最小平均差异的集群被称为相邻簇(neighboring cluster),也就是下一个最近的簇
下面我们定义样本点\(x_i\)的轮廓值silhouette
\[{\displaystyle s(x_i)={\frac {b(x_i)-a(x_i)}{\max\{a(x_i),b(x_i)\}}}} ,x_i \in C_p , \text{if } |C_p| > 1\]
也可以写作(这里简写了样本点)
\[s(i) = \begin{cases} 1-a(i)/b(i), & \text{if } a(i) < b(i) \\ 0, & \text{if } a(i) = b(i) \\ b(i)/a(i)-1, & \text{if } a(i) > b(i) \\ \end{cases}\]
metrics.silhouette_score
-
Dunn指数(Dunn index, DI)
\[DI=\min_{1\leq i\leq k}\bigg\{ \min_{j\neq i}\bigg(\frac{d_{min}(C_i,C_j)}{\max_{1\leq l \leq k}diam(C_l)}\bigg) \bigg\}\]
DI值越大越好,解释同DBI -
CH指数(Calinski-Harabasz Index)
该指数是所有簇的簇间离散度(between-clusters dispersion)和簇内离散度(within-cluster dispersion)之和的比值(其中离散度定义为距离平方和)
\[s = \frac{\mathrm{tr}(B_k)/{k - 1}}{\mathrm{tr}(W_k) / {n_E - k}} = \frac{\mathrm{tr}(B_k)}{\mathrm{tr}(W_k)} \times \frac{n_E - k}{k - 1} \]
其中两个矩阵(类间离散度矩阵\(B_k\)和类内离散度矩阵\(W_k\))的定义
\[W_k = \sum_{q=1}^k \sum_{x \in C_q} (x - c_q) (x - c_q)^T\]
\[B_k = \sum_{q=1}^k n_q (c_q - c_E) (c_q - c_E)^T\]
\(\mathrm{tr}(B_k)\)表示矩阵的迹;
大\(C_q\)表示簇\(q\)的集合;小\(c_q\)表示簇\(q\)的中心;小\(c_E\)表示数据集\(E\)的中心;
\(n_q\)表示簇\(q\)的数量;\(E\)表示数据集;\(n_E\)表示数据集\(E\)的数量;\(k\)表示簇的个数;
该指数越大越好
metrics.calinski_harabasz_score
External evaluation(就是需要人为标记每个样本所属的类)
有监督的方法,需要基准数据或者参考模型。用一定的度量评判聚类结果与基准数据的符合程度。(基准是一种理想的聚类,通常由专家构建)
-
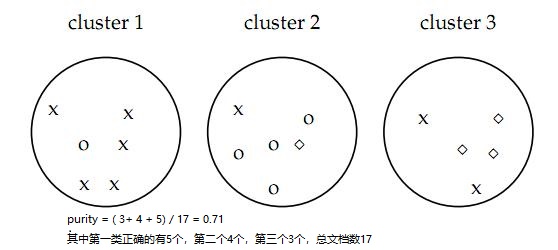
纯度(Purity)
我们假定数据集有N个数据。分类classes使用\(C = \{c_i|i=1,…,n \}\);聚类clusters结果\(K= \{k_i|1,…,m\}\);
purity方法是极为简单的一种聚类评价方法,只需计算正确聚类的文档数占总文档数的比例:
\[{\displaystyle {\frac {1}{N}}\sum _{k_i\in K}\max _{c_j\in C}{|k_i\cap c_j|}}\]
值在[0,1]之间,完全错误的聚类方法值为0,完全正确的方法值为1
-
F-score
F1 score, also known as balanced F-score or F-measure
\[P(\text{precision rate})={\frac {TP}{TP+FP}}, R(\text{recall rate})={\frac {TP}{TP+FN}}\]
\[F_{\beta }={\frac {(\beta ^{2}+1)\cdot P\cdot R}{\beta ^{2}\cdot P+R}}\]
F1 score就是\(\beta = 1\)时的F-measure;当\(\beta = 0, F_0=P\);
Precision and recall
metrics.f1_score
- Jaccard index
\[{\displaystyle {\text{Jaccard index}}=J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {TP}{TP+FP+FN}}}\]
metrics.jaccard_score
-
\[{\displaystyle DSC={\frac {2TP}{2TP+FP+FN}}}\]
-
Homogeneity, completeness and V-measure
同质性(Homogeneity):每一个cluster(聚类结果簇)中所包含的数据应归属于一个class(类)。
完整性(completeness):所有属于同一个class的数据应该被归到相同的cluster中。
我们假定数据集有N个数据。分类classes使用\(C = \{c_i|i=1,…,n \}\);聚类clusters结果\(K= \{k_i|1,…,m\}\);
\(A = [a_{ij}]_{n \times m}\),其中 \(a_{ij}\) 表示\(c_i\)属于\(k_j\)的数量(就是contingency table,下面有讲)
\[h = 1 - \frac{H(C|K)}{H(C)} , c = 1 - \frac{H(K|C)}{H(K)}\]
\[H(C|K) = - \sum_{k=1}^{|K|} \sum_{c=1}^{|C|} \frac{a_{ck}}{N} \cdot \log\left(\frac{a_{ck}}{\sum_{c=1}^{|C|}a_{ck}}\right) \quad,\quad H(C) = - \sum_{c=1}^{|C|} \frac{\sum_{k=1}^{|K|}a_{ck}}{N} \cdot \log\left(\frac{\sum_{k=1}^{|K|}a_{ck}}{N}\right)\]
metrics.homogeneity_score, metrics.completeness_score, metrics.v_measure_score
三个指数一起返回metrics.homogeneity_completeness_v_measure
- Rand指数(Rand index)
\[RI={\frac {TP+TN}{TP+FP+FN+TN}}=\frac{a+d}{n(n-1)/2}\]
[0,1]区间,值越大越好
衡量两个数据聚类之间相似性的度量(也可以是标记数据和预测数据之间的相似性)
1.0 是完美匹配分数。未调整 Rand 指数的得分范围为 [0, 1],调整后(adjusted)的 Rand 指数为 [-1, 1]
metrics.rand_score 、metrics.adjusted_rand_score
- FM指数(Fowlkes–Mallows index)
\[\text{FMI} = \frac{\text{TP}}{\sqrt{(\text{TP} + \text{FP}) (\text{TP} + \text{FN})}}\]
metrics.fowlkes_mallows_score
- 情形分析表(Contingency Matrix)
from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [0, 0, 1, 1, 2, 2]
contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])
列数代表y中不重复的个数;行代表x中不重复的个数;
第一行分别表示:2个a属于0,1个a属于1,0个a属于2
第二行分别表示:0个b属于0,1个b属于1,2个b属于2
metrics.cluster.contingency_matrix
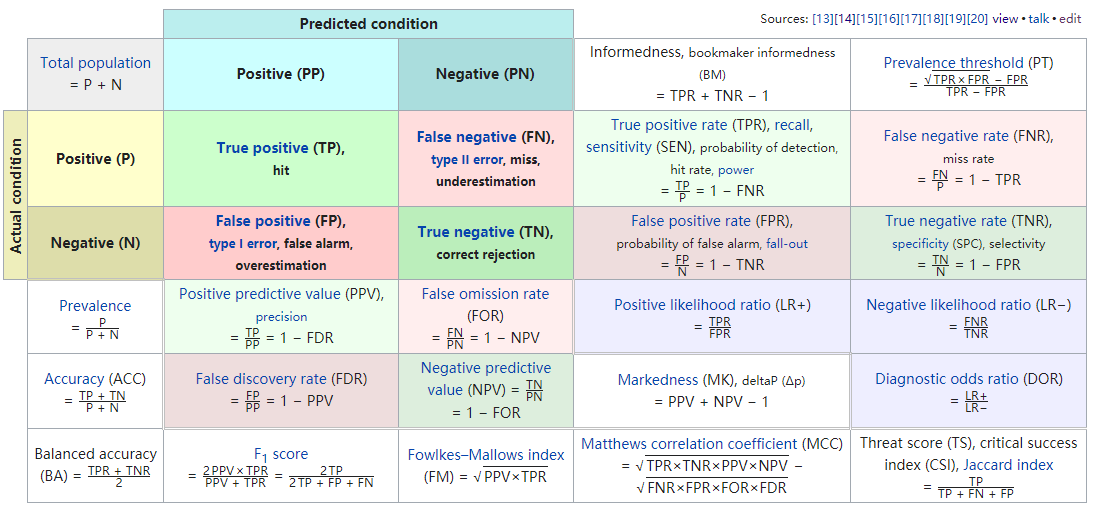
- 混淆矩阵(Confusion matrix)
行Predicted (expectation)
列Actual (observation)
TN表示预测negative正确
TP表示预测positive正确
FN表示预测negative错误
FP表示预测positive错误
| Actual\Predicted | P | N |
|---|---|---|
| P(positive) | TP | FN |
| N(negative) | FP | TN |
注意正常的confusion matrix中的四个元素相加为\(C_n^2=n(n-1)/2\),而pair_confusion_matrix是\((n-1)\),并且混淆矩阵
\[\begin{split}C = \left[\begin{matrix} C_{00}(FN) & C_{01}(FP) \\ C_{10}(TN) & C_{11}(TP) \end{matrix}\right]\end{split}\]
- 互信息(mutual information)
数据集\(S=\{s_{1},s_{2},\ldots s_{N}\}\), 簇\(U=\{U_{1},U_{2},\ldots ,U_{R}\}\)以及簇\(V=\{V_{1},V_{2},\ldots ,V_{C}\}\),满足\({\displaystyle U_{i}\cap U_{j}=\varnothing =V_{i}\cap V_{j}}\)以及\(\cup _{{i=1}}^{R}U_{i}=\cup _{{j=1}}^{C}V_{j}=S\)
有这样一个表(R*C)\(M=[n_{{ij}}]_{{j=1\ldots C}}^{{i=1\ldots R}}\),称为contingency table,其中\(n_{{ij}}=\left|U_{i}\cap V_{j}\right|\)
\({\displaystyle P_{U}(i)={\frac {|U_{i}|}{N}}}\)表示随机选取一个数据,属于\(U_i\)簇的概率。
\({\displaystyle P_{UV}(i,j)={\frac {|U_{i}\cap V_{j}|}{N}}}\)表示随机选取一个数据,同时属于\(U_i, V_j\)簇的概率。
\({\displaystyle H(U)=-\sum _{i=1}^{R}P_{U}(i)\log P_{U}(i)}\)表示\(U\)的熵。
\[{\displaystyle MI(U,V)=\sum _{i=1}^{R}\sum _{j=1}^{C}P_{UV}(i,j)\log {\frac {P_{UV}(i,j)}{P_{U}(i)P_{V}(j)}}}\]
\[\text{NMI}(U, V) = \frac{\text{MI}(U, V)}{\text{mean}(H(U), H(V))}\]
\[AMI(U,V)={\frac {MI(U,V)-E\{MI(U,V)\}}{\max {\{H(U),H(V)\}}-E \{MI(U,V)\}}}\]
其中
\[{\begin{aligned}E\{MI(U,V)\}=&\sum _{{i=1}}^{R}\sum _{{j=1}}^{C}\sum _{{n_{{ij}}=(a_{i}+b_{j}-N)^{+}}}^{{\min(a_{i},b_{j})}}{\frac {n_{{ij}}}{N}}\log \left({\frac {N\cdot n_{{ij}}}{a_{i}b_{j}}}\right)\times \\&{\frac {a_{i}!b_{j}!(N-a_{i})!(N-b_{j})!}{N!n_{{ij}}!(a_{i}-n_{{ij}})!(b_{j}-n_{{ij}})!(N-a_{i}-b_{j}+n_{{ij}})!}}\\\end{aligned}}\]
\(E\{MI(U,V)\} 为MI(U,V)\)的期望;\((a_{i}+b_{j}-N)^{+} = \max(1,a_{i}+b_{j}-N)\);
\(a_{i}=\sum _{{j=1}}^{C}n_{{ij}}\);\(b_{j}=\sum _{{i=1}}^{R}n_{{ij}}\)
越大越好,最好为1
参考Adjusted mutual information
metrics.adjusted_mutual_info_score,metrics.normalized_mutual_info_score,metrics.mutual_info_score
Cluster tendency(聚类趋势)
- 霍普金斯统计量(Hopkins statistic)
聚类趋势(聚类可行性):应用聚类算法之前,应该考虑聚类可行性;如:即使数据不包含任何cluster,聚类方法也会返回cluster;因此,评估数据集是否包含有意义的cluster(即:非随机结构)有时会变得有必要。此过程被定义为 聚类趋势的评估 或 聚类可行性的分析。
与非随机结构相对的是均匀分布(随机结构),霍普金斯统计量的计算原理,便是检查数据是否符合均匀分布(或者说随机性)。
有数据集\(X=\{x_1,x_2,...,x_n\},x_i \in \mathbb{R}^d\)
生成随机数据集\(Y=\{y_1,y_2,...,y_m\}, m \ll n \),即从样本的可能取值范围内随机生成m个点
\(u_{i} = \min dist(y_i,x_j\in X)\)就是一个随机点与数据集X中的点的最小距离;
从所有样本中随机找m个点,\(w_{i} = \min dist(x_i,x_j\in X_{i\neq j})\)就是每个点在样本空间(X)中找到一个离他最近的点之间的距离;
\[{\displaystyle H={\frac {\sum _{i=1}^{m}{u_{i}^{d}}}{\sum _{i=1}^{m}{u_{i}^{d}}+\sum _{i=1}^{m}{w_{i}^{d}}}}\,,}\]
随机生成的点(样本可能的取值范围内)与从样本中找出点的空间比值
根据这个定义,均匀随机数据的值应该趋向于接近0.5(不可行),而聚集数据的值应该趋向于接近1(可行)【\(\sum u \gg \sum w\),也就是说,如果聚类趋势明显,则随机生成的样本点距离应该远大于实际样本点的距离】。
参考Clustering performance evaluation以及Evaluation and assessment
k-means: 样本集合\(X=\{x_1,x_2,...,x_n\},x_i \in \mathbb{R}^m\),算法的目标是将n个样本分到不同的cluster中\(C = \{ C_1,...,C_k\},k \lt n,C_i \cap C_j =\empty , \cup_{i=1}^kC_i =X\);
用\(F: x_i \to l,l\in \{1,...,k\}\)表示划分函数,输入样本,输出所在的cluster
-
模型:
\[l = F(x_i) = F(i) ,i \in \{1,...,n\} \] -
策略:
\[F^* = \argmin_{F} W(F) = \argmin_{F} \sum_{l=1}^k \sum_{F(i)=l}^{n_l} \|x_i - \bar{x}_l\|^2\]
其中损失函数\(W(F)\)为样本与其所属cluster的中心之间的距离的总和;
\(n_l = \sum_{i=1}^n I(F(i)=l)\);
n个样本分到k个cluster的所有分法的种类有\(S(n,k)\)种,这个数字是指数级的,所以最优问题是个NP困难问题
- 算法:
迭代算法,不能保证全局最优
- 随机选择k个中心\((m_1,m_2,...,m_k)\),
- 将样本分别划分到与其最近的中心的cluster中
- 更新每个cluster的均值\((m_1,m_2,...,m_k)\)作为cluster的新的中心
- 重复2,3直到收敛(中心变化很小)
K-means算法有以下不足:
- 算法对初始值的选取依赖性极大。初始值不同,往往得到不同的局部极小值。
- 由于将均值点作为聚类中心进行新一轮计算,远离数据密集区的孤立点和噪声点会导致聚类中心偏离真正的数据密集区,所以K-均值算法对噪声点和孤立点很敏感。
K-mediods算法优缺点
K-中心点轮换算法是一种使目标函数下降最快的方法,它属于启发式搜索算法,能从n个对象中找出以k个中心点为代表的一个局部优化划分聚类。与K-均值算法比较,K-中心点轮换算法解决了K-均值算法本身的缺陷:
- 解决了K-均值算法对初始值选择依赖度大的问题。K-均值算法对于不同的初始值,结果往往得到不同的局部极小值。而K-中心点轮换算法采用轮换替换的方法替换中心点,从而与初始值的选择没有关系。
- 解决了K-均值算法对噪声和离群点的敏感性问题。由于该算法不使用平均值来更改中心点而是选用位置最靠近中心的对象作为中心代表点,因此并不容易受极端数据的影响,具有很好的鲁棒性。
K-中心点轮换算法也存有以下缺点:
- 由于K-中心点轮换算法是基于划分的一种聚类算法,仍然要求输入要得到的簇的数目k,所以当k的取值不正确时,对聚类的结果影响甚大。
- 从以上的时间复杂度也可以看出,当n和k较大时,计算代价很高,所以将该算法应用于大数据集时不是很理想。
参考文献
[14-1] Jain A, Dubes R. Algorithms for clustering data. Prentice-Hall, 1988.
[14-2] Aggarwal C C, Reddy C K. Data clustering: algorithms and applications. CRC Press, 2013.
[14-3] MacQueen J B. Some methods for classification and analysis of multivariate observations. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Volume 1,pp.396-410. 1967.
[14-4] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction. Springer. 2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[14-5] Pelleg D, Moore A W. X-means: Extending K-means with Efficient Estimation of the Number of Clusters. Proceedings of ICML, pp. 727-734, 2000.
[14-6] Ester M, Kriegel H, Sander J, et al. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Proceedings of ACM SIGKDD, pp. 226-231, 1996.
[14-7] Shi J, Malik J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000,22(8):888-905.
[14-8] Dhillon I S. Co-clustering documents and words using bipartite spectral graph partitioning. Proceedings of ACM SIGKDD, pp. 269-274. 2001.