Table of Contents

• • 第 15 章 奇异值分解
    • 附加知识
      • 矩阵性质
        • 共轭转置（Conjugate transpose）
        • 埃尔米特矩阵（Hermitian matrix）
        • Normal matrix
        • 酉矩阵（Unitary matrix）
      • 矩阵分解(因子分解)
    • 参考文献
  • 第 16 章 主成分分析
    • 附加知识
      • 基变换
      • 协方差
        • 协方差矩阵
        • 期望
        • 方差
      • 有偏估计和无偏估计
      • 因子分析FA
      • 独立成分分析ICA
    • 参考文献
  • 第 17 章 潜在语义分析
    • 参考文献
  • 第 18 章 概率潜在语义分析
    • 参考文献

第 15 章 奇异值分解

奇异值分解(Singular Value Decomposition, SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。也是矩阵分解（Matrix decomposition）的一种。

先了解下特征值分解（Eigenvalues and eigenvectors以及Eigendecomposition of a matrix）以及对角化（Diagonalizable matrix）
特征值（有些方阵是没有特征值的）：

特征值分解：
设\(A_{n\times n}\)，是具有n个线性无关的特征向量\(q_i\)（不一定是不同特征值,可以有相同的特征值），那么A可以分解为：

其中A是方阵，\(\Lambda\)是由特征值组成的对角矩阵（diagonal matrix）；
\(q_i\)通常是标准化的，但不是必须的;
因为Q的列是线性无关的，所以 Q 是可逆的;
如果A的特征值都不为0那么A是可逆的（invertible）\({\displaystyle \mathbf {A} ^{-1}=\mathbf {Q} \mathbf {\Lambda } ^{-1}\mathbf {Q} ^{-1}}\)

注意只有可对角化的矩阵分解才能用这种方式：如以下矩阵不可被对角化

其特征值为\([1,1]\),特征向量为\([1,0]^T , [-1,0]^T\)

如果 \(\mathbf {A}\) 是对称矩阵（symmetric matrix），因为\(\mathbf {Q}\) 由特征向量构成 \(\mathbf {A}\) 它保证是一个正交矩阵（orthogonal matrix）,有\({\displaystyle \mathbf {Q} ^{-1}=\mathbf {Q} ^{\mathrm {T} }}\)

Q其实也是酉矩阵（Unitary Matrix），它是 正交矩阵 在复数上的推广。

不可对角化的矩阵称为有缺陷的（defective）。对于有缺陷的矩阵，特征向量的概念推广到广义特征向量（generalized eigenvectors），特征值的对角矩阵推广到Jordan 范式（Jordan normal form）。在代数闭域上，任何矩阵A都具有Jordan 范式，因此允许广义特征向量的基和分解为广义特征空间（generalized eigenspaces）。

• 模型：
  对于复矩阵 \(M_{m \times n} = {\displaystyle \mathbf {U\Sigma V^{H}} }\)
  对于实矩阵 \(M_{m \times n} = {\displaystyle \mathbf {U\Sigma V^{T}} }\)
  其中\(U\)是\({\displaystyle m\times m}\)复酉矩阵(正交矩阵)
  \(\Sigma = diag(\sigma_1,\sigma_2,...,\sigma_p)\)是矩形对角矩阵（rectangular diagonal matrix），对角元素是非负的实数并且降序排列,\(p=\min(m,n), \sigma_1 \ge \sigma_2 \ge ... \ge \sigma_p \ge 0\)
  \(V\)是一个\({\displaystyle n\times n}\)复酉矩阵(正交矩阵)
  \(\sigma_i\)称为矩阵M的奇异值
  \(U\)的列向量称为左奇异向量left-singular vector
  \(V\)的列向量称为右奇异向量right-singular vector
  如果矩阵\(M\)的秩为\(r = rank(M),r \le \min(m,n)\)
  \(M\)的紧SVD（compact SVD）为\(M_{m \times n} = U_{m \times r} \Sigma_{r \times r} V_{n \times r}^T\)，\(rank(\Sigma_{r \times r}) = rank(M) = r\)（可以无损压缩）
  \(M\)的截断SVD（truncated SVD）为\(M_{m \times n} \approx U_{m \times k} \Sigma_{k \times k} V_{n \times k}^T , 0 \lt k \lt r\)（有损压缩）
  矩阵\(M\)的伪逆（pseudoinverse）\(M^{+} = V\Sigma^{+}U^{H}\)
  \(M\)的奇异值\(\sigma_i\)是\(M^TM\)的特征值的平方根\(\sqrt{\lambda_i}\),\(V\)的列向量是\(M^TM\)的特征向量，\(U\)的列向量是\(MM^T\)的特征向量
  \(M^TM\)很明显还是一个对称矩阵，其特征值为非负，证明：假设\(\lambda\)是\(M^TM\)的一个特征值
  \(\|Mx\|^2 = x^TA^TAx = x^T \lambda x= \lambda x^Tx = \lambda\|x\|^2 \Rightarrow \lambda = \frac{\|Mx\|^2}{\|x\|^2} \ge 0\)
  

  \[{\begin{aligned}\mathbf {M} ^{T}\mathbf {M} &=\mathbf {V} {\boldsymbol {\Sigma }}^{T}\mathbf {U} ^{T}\,\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{T}=\mathbf {V} ({\boldsymbol {\Sigma }}^{T}{\boldsymbol {\Sigma }})\mathbf {V} ^{T}\\\mathbf {M} \mathbf {M} ^{T}&=\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{T}\,\mathbf {V} {\boldsymbol {\Sigma }}^{T}\mathbf {U} ^{T}=\mathbf {U} ({\boldsymbol {\Sigma }}{\boldsymbol {\Sigma }}^{T})\mathbf {U} ^{T}\end{aligned}}\]
  
  这不就是矩阵的特征值分解吗【上面有将特征值分解有讲到对称矩阵的对角化（特征值分解）】

• 策略：

• 算法：

附加知识

矩阵性质

这里介绍一些参见的矩阵，以及其性质。

共轭转置（Conjugate transpose）

共轭（Complex conjugate）是复数上的概念
对于一个复数\(z =a + bi\)，其共轭为\(\bar{z} = a-bi\)，所以有\(z\bar{z} = a^2 + b^2\)
共轭转置也有其它叫法，如：Hermitian conjugate, bedaggered matrix, adjoint matrix or transjugate。值得注意的是adjoint matrix而不是 这个Adjugate matrix，虽然有时候他们都用\(A^*\)表示。这里为了统一我用\(A^H\)表示A的共轭转置矩阵。可以参考共轭转置矩阵与伴随矩阵都用A*表示合理吗？

有个神奇的公式：欧拉公式 \(e^{\pi i}+1=0\) ，准确的说欧拉公式为：\(e^{ix}=\cos x + i\sin x\)，前面只是当\(x=\pi\)时的结果。
这个公式里既有自然底数e，自然数1和0，虚数i还有圆周率pi，它是这么简洁，这么美丽啊！

例如：

性质：

• \({\displaystyle ({\boldsymbol {A}}+{\boldsymbol {B}})^{\mathrm {H} }={\boldsymbol {A}}^{\mathrm {H} }+{\boldsymbol {B }}^{\mathrm {H} }}\)
• \({\displaystyle (z{\boldsymbol {A}})^{\mathrm {H} }={\overline {z}}{\boldsymbol {A}}^{\mathrm {H} }}\)
• \({\displaystyle ({\boldsymbol {A}}{\boldsymbol {B}})^{\mathrm {H} }={\boldsymbol {B}}^{\mathrm {H} }{\boldsymbol {A}} ^{\mathrm {H} }}\)
• \({\displaystyle \left({\boldsymbol {A}}^{\mathrm {H} }\right)^{\mathrm {H} }={\boldsymbol {A}}}\)
• 如果\(A\)可逆，当且仅当\(A^H\)可逆，有\({\displaystyle \left({\boldsymbol {A}}^{\mathrm {H} }\right)^{-1}=\left({\boldsymbol {A}}^{-1}\right)^{ \mathrm {H} }}\)
• \(A^H\)的特征值是\(A\)特征值的复共轭
• 内积性质\({\displaystyle \left\langle {\boldsymbol {A}}x,y\right\rangle _{m}=\left\langle x,{\boldsymbol {A}}^{\mathrm {H} }y\right\rangle _{n}}\)，A是m*n,x是n*1,y是m*1，下标m表示是m维向量作内积。
• （A是方阵）行列式性质\({\displaystyle \det \left({\boldsymbol {A}}^{\mathrm {H} }\right)={\overline {\det \left({\boldsymbol {A}}\right)}}}\)
• （A是方阵）迹的性质\({\displaystyle \operatorname {tr} \left({\boldsymbol {A}}^{\mathrm {H} }\right)={\overline {\operatorname {tr} ({\boldsymbol {A}})}}}\)

埃尔米特矩阵（Hermitian matrix）

Hermitian matrix (or self-adjoint matrix)
A是复方阵

例子：

埃尔米特矩阵是对称矩阵在复数上的推广。

其矩阵有很多性质，具体见维基百科。

Skew-Hermitian matrix：\({\displaystyle A{\text{ skew-Hermitian}}\quad \iff \quad A^{\mathsf {H}}=-A}\)

Normal matrix

A是复方阵

例子：

Normal matrix一定是可对角化的\(A = U\Lambda U^H\)，\(U\)是酉矩阵，\(\Lambda = diag(\lambda_1,...)\)是\(A\)的特征值组成的对角矩阵

对于复矩阵，所有的unitary, Hermitian, and skew-Hermitian 矩阵都是normal矩阵
对应的对于实矩阵，所有的 orthogonal, symmetric, and skew-symmetric 矩阵也都是normal矩阵

酉矩阵（Unitary matrix）

U是复方阵

性质：

• \({\displaystyle U^{H}U=UU^{H}=I,}\)
• \(\left\langle Ux,Uy\right\rangle = \left\langle x,y\right\rangle\)
• U是可对角化的\({\displaystyle U=VDV^{H},}\)where V is unitary, and D is diagonal and unitary.
• \({\displaystyle \left|\det(U)\right|=1}\)
• 其特征向量是相互正交的（废话，正交矩阵的推广）

酉矩阵它是正交矩阵在复数上的推广。

矩阵分解(因子分解)

sympy.Matrix除了分解还有diagonalize对角化（也是一种矩阵分解），eig特征值（其实也可以特征值分解），rref行简化阶梯型，det行列式，inv逆矩阵，广义逆矩阵pinv；更多参考
scipy.linalg中也有很多关于线性代数的方法：scipy.linalg.svd，以及各种矩阵分解的方法；更多参考
numpy.linalg中也有很多关于线性代数的方法：np.linalg.svd；更多参考

除了SVD和PCA，还有很多矩阵分解（Matrix decomposition）的方法。不过有很多分解是有要求的，比如必须是方阵（特征值分解就要求必须是方阵）等。

• LU分解（LU decomposition）
  

  \[{\displaystyle A=LU.}\]
  
  L是下三角矩阵（lower triangular matrix）
  U是上三角矩阵（upper triangular matrix）
  有时还会包含一个置换矩阵（permutation matrix），它在每行和每列中只有一个1，而在其他地方则为0。
  
  \[{\displaystyle A=PLU}\]

• QR分解（QR decomposition）
  

  \[A = QR\]
  
  Q是正交矩阵（Orthogonal Matrix）；
  R是上三角矩阵（right(upper) triangular matrix）

类似的可以定义QL、RQ 和 LQ，L是下三角矩阵（left(lower) triangular matrix）

• 非负矩阵分解（Non-negative matrix factorization (NMF or NNMF)）
  
  \[\mathbf {A} =\mathbf {W} \mathbf {H} \,.\]
  
  将矩阵\(A\)分解为两个非负矩阵的乘积(近似相等)
  
  \[minimize {\displaystyle \left\|V-WH\right\|_{F},} \\ s.t. W\geq 0,H\geq 0.\]
  
  这里有讲到不同的表示方法对应这不同说法，这里有不同的表示方法

参考文献

[15-1] Leon S J. Linear algebra with applications. Pearson, 2009(中译本：线性代数。张文博，张丽静 译. 北京：机械工业出版社)

[15-2] Strang G. Introduction to linear algebra. Fourth Edition. Wellesley-Cambridge Press, 2009.

[15-3] Cline A K. Dhillon I S. Computation of the singular value decomposition, Handbook of linear algebra. CRC Press, 2006.

[15-4] 徐树方. 矩阵计算的理论与方法。北京：北京大学出版社, 1995.

[15-5] Kolda T G,Bader B W. Tensor decompositions and applications. SIAM Review, 2009, 51(3):455-500.

第 16 章 主成分分析

主成分分析（Principal component analysis, PCA）是一种常用的无监督学习方法，PCA利用正交变换把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，线性无关的变量称为主成分。

主成分分析步骤如下：

1. 对给定数据进行规范化，使得数据每一变量的平均值为0,方差为1（StandardScaler）。

2. 对数据进行正交变换，原来由线性相关变量表示的数据,通过正交变换变成由若干个线性无关的新变量表示的数据。

新变量是可能的正交变换中变量的方差的和(信息保存)最大的，方差表示在新变量上信息的大小。将新变量依次称为第一主成分、第二主成分等。

我们通常表示一个样本是在实数空间中用正交坐标系表示，规范化的数据分布在原点附近

主成分分析就是对数据进行正交变换，对原坐标系进行旋转变换，并将数据在新坐标系中表示；我们将选择方差最大的方向作为新坐标系的第一坐标轴。方差最大代表着在该方向上的投影（不就是在这个坐标系的坐标轴上的表示么）分散的最开。

根据方差的定义，每个方向上方差就是在该坐标系（变换后的新坐标系）上表示所对应的维度的方差\(var(a) = \frac{1}{N-1}\sum_{i=1}^N (a_i - \mu)^2\)（用第一个方向来说明, N个样本的第一个维度组成向量\(a\)）；由于我们已经对数据进行的规范化，所以均值为0；\(var(a) = \frac{1}{N-1}\sum_{i=1}^N (a_i)^2\) ;\(a_i\)就是第\(i\)个样本\(x^{(i)}\)与第一个方向的内积。

我们的目的就是为了\(var(a)\)最大，我们要求的就是找到变换后的新坐标系，假设方差最大的方向的单位向量为\(v_1\)，数据集\(T = \{x^{(1)},x^{(2)},...,x^{(N)}\} , x=\{x_1,...,x_m\}^T\)，m维

设矩阵\(X = [x^{(1)},x^{(2)},...,x^{(N)}]\)那么\(XX^T =\sum_{i=1}^N[{x^{(i)}}{x^{(i)}}^{T}]\)，得到

拉格朗日函数（参见矩阵求导）



其实\(\frac{1}{N-1}XX^T\)就是\(X_{m \times N}\)样本的协方差矩阵\(\Sigma_{m \times m}\)

\(\lambda_1\)是\(\Sigma_{m \times m}\)的特征值，\(v_1\)(列向量)是其对应的特征值向量；

接着求第二个主成分\(v_2\),主成分是相互正交的

注意到

依次求得其它成分。

最终有主成分组成的矩阵
\(V_{m \times m } = [v_1,v_2,...,v_m]\)
降维到k维就是一次取前k个向量组成的矩阵与X作乘积，那么降维后的数据：

前面学习了SVD需要求\(A^TA\)的特征值分解;而PCA需要求\(\frac{1}{N-1}XX^T\)的特征值分解;
只需要取\(A = \frac{X^T}{\sqrt{N-1}}\)就可以将PCA问题可以转化为SVD问题求解
其实，PCA只与SVD的右奇异向量的压缩效果相同。
一般 \(X\) 的维度很高，\(XX^T\) 的计算量很大，并且方阵的特征值分解计算效率不高，SVD除了特征值分解这种求解方式外，还有更高效且更准确的迭代求解法，避免了\(XX^T\)的计算

• 模型：
• 策略：
• 算法：

稀疏主成分分析（Sparse PCA）
稀疏 PCA 问题有许多不同的公式，以下是使用Structured Sparse Principal Component Analysis以及Online Dictionary Learning for Sparse Coding

意思就是求UV让其近似等于X，然后得到一个稀疏矩阵V
sklearn.decomposition.SparsePCA.components_ 就是其稀疏的矩阵\(V\)
SPCA的含义参考 Matrix decomposition

附加知识

基变换

我们常说的向量(3,2)其实隐式引入了一个定义：以 x 轴和 y 轴上正方向长度为 1 的向量为标准。向量 (3,2) 实际是说在 x 轴投影为 3 而 y 轴的投影为 2。注意投影是一个标量，所以可以为负。
而x 轴和 y 轴的方向的单位向量就是(1,0)和(0,1)，所以(1,0)和(0,1)就是坐标系的基

如：另一组基(单位向量)\((\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)和\((-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)
那么(3,2)在该坐标系中如何表示呢？我们知道一个向量\(a\)在一个方向（\(单位向量x\)）上的投影可以用内积表示\(\braket{a,x} = \|a\|.\|x\|\cos \theta = \|a\|\cos \theta\)，其中\(\theta\)表示两个向量的夹角。

\(a=(3,2)\)在\(x=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)这个方向的投影为\(\braket{a,x} = \frac{5}{\sqrt{2}}\)
\(a=(3,2)\)在\(y=(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)这个方向的投影为\(\braket{a,y} = -\frac{1}{\sqrt{2}}\)

所以新坐标为\((\frac{5}{\sqrt{2}},-\frac{1}{\sqrt{2}})\)

我们也可以用矩阵来表示(x,y是行向量;a用列向量)

协方差

协方差（Covariance）的定义：

性质：

协方差矩阵

协方差矩阵（Covariance matrix）的定义：对称的方阵
\(X\)是个随机向量（random vector），每个实体（随机变量）就是一个列向量，就是矩阵用列向量表示；

\(X\)的协方差矩阵用\({\displaystyle \operatorname {K} _{\mathbf {X} \mathbf {X} }}\)表示，矩阵中的每个元素\({\displaystyle \operatorname {K} _{X_{i}X_{j}}=\operatorname {cov} [X_{i},X_{j}]=\operatorname {E} [(X_{i}-\operatorname {E} [X_{i}])(X_{j}-\operatorname {E} [X_{j}])]}\)

样本的协方差（无偏）

样本的协方差矩阵：

这里很多协方差函数都有参数，可以设置到底是按行向量还是列向量计算协方差。
也有些地方是用\(\frac{1}{n}\)，就是无偏与有偏的区别。

\(\text{np.cov}(X_{3 \times 2},rowvar = False)\)输出\(2 \times 2\)（rowvar = False表示一列是一个特征）;默认是输出\(3 \times 3\)（默认是行表示一个特征）
\(\text{np.cov}(x,y,z)\)输出\(3 \times 3\)

期望

期望（Expectation）的定义：

性质：

如果\(X,Y\)是相互独立的，那么\({\displaystyle \operatorname {E} [XY]=\operatorname {E} [X]\operatorname {E} [Y]}\)

常数的期望等于常数本身\(E(a) = a\)

\(x_i\)是随机变量\(X\)的一个实例，\(X\)服从什么分布，\(x_i\)也是服从什么分布的，所以\(E(x_i) = E(X),D(x_i) = D(X)\)

\(E(X)\)为一阶矩
\(E(X^2)\)为二阶矩

原点矩（raw moment）和中心矩（central moment）
\(E(X^k)\)为k阶远点矩，一阶原点矩是数学期望
\(E(X-E(X))^k\)为k阶中心矩，二阶原点矩是方差（以\(E(X)\)为中心）

方差

方差（Variance）的定义：

性质：
\(D(X)\) 和 \(Var(X)\) 都是表示方差；方差大于等于0；参数的方差为0；

\(\operatorname {Var} (X)=\operatorname {Cov} (X,X).\)

\(\operatorname {Var} (X+a)=\operatorname {Var} (X).\)
\(\operatorname {Var} (aX)=a^{2}\operatorname {Var} (X).\)
\(\operatorname {Var} (aX+bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)+2ab\,\operatorname {Cov} (X,Y),\)
\(\operatorname {Var} (aX-bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)-2ab\,\operatorname {Cov} (X,Y),\)

\({\displaystyle \operatorname {Var} (XY)=\operatorname {E} \left(X^{2}\right)\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (X)]^{2}[\operatorname {E} (Y)]^{2}.}\)

有偏估计和无偏估计

参数估计需要未知参数的估计量和一定置信度
估计方法：用点估计估计一个值；用区间估计估计值的可能区间和是该值的可能性。
估计的偏差的定义：

\(\theta\)是数据分布真实参数（完美）
\(\theta\)的估计量或统计量\(\hat{\theta}_m\)

对估计值的评价标准：

• 无偏性（Unbiasedness）：是估计量（不一定是样本均值）抽样分布的数学期望等与总体参数的真值。
  \(m\)为样本数量（抽样数量）
  如果\(bias(\hat{\theta}_m) = 0\)那么估计量\(\hat{\theta}_m\)被称为无偏(unbiased)的,意味着\(E(\hat{\theta}_m) = \theta\)
  如果\(\lim_{m \to \infty}bias(\hat{\theta}_m) = 0\)那么估计量\(\hat{\theta}_m\)被称为 渐近无偏 (asymptotically unbiased) 的,意味着 \(\lim_{m \to \infty}E(\hat{\theta}_m) = \theta\)

• 有效性（Efficiency）：是有时几组数据都是无偏的，但是此时有效数是方差最小的。
  如：样本\((x_1,...,x_m)\)，其均值为\(\mu\)，方差为\(\sigma^2\)
  第一种情况：随机取一个样本\(x_i\)，那么\(E(x_i)=E(x_1)=...=\mu\)，方差为\(D(x_i)=D(x_1)=...=\sigma^2\)（因为每个值都有可能取到，所以随机取一个样本得期望就是均值，方差就是\(\sigma^2\)）
  第二种情况：取平均值\(\bar{x}\),那么\(E(\bar{x}) = E[\frac{1}{m}\sum_m x_i] =\frac{1}{m}E[\sum_mx_i] = \frac{1}{m}[\sum_mE(x_i)] = \frac{1}{m}[\sum_m \mu] = \mu\);
  \(D(\bar{x}) = D(\frac{1}{m}\sum_m x_i) = \frac{1}{m^2}D(\sum_m x_i) = \frac{1}{m^2}\sum_m D(x_i) = \frac{1}{m^2} m\sigma^2 = \frac{\sigma^2}{m}\)
  很明显第二种的方差小

• 一致性（Consistency）：是指样本变大，估计越准。
  \(\lim_{m \to \infty}P(|\hat{\theta}_m - \theta | \lt \epsilon) = 1\)

无偏估计
例如样本均值的估计为\(\hat{\mu} = \sum_{i=1}^m x_i\)，真实的均值为\(\mu\)，如何知道这个估计是有偏还是无偏？根据定义判断偏差是否为0；\(bias(\hat{\mu}) = E(\hat{\mu}) - \mu\)
这里的证明再有效性已经证明过了。

有偏估计
如果样本方差的估计为\(\hat{\sigma}^2 = \frac{1}{m}\sum_{i=1}^m(x_i-\hat{\mu})^2\),\(\hat{\mu} = \sum_{i=1}^m x_i\)，那么偏差\(bias(\hat{\sigma}^2) = E[\hat{\sigma}^2] - \sigma^2\)不为0，就证明这个估计是有偏的。
我们来求\(E[\hat{\sigma}^2]\)

\(E[\hat{\mu}^2] = D(\hat{\mu}) + E(\hat{\mu})^2\)
而\(D(\hat{\mu}) = \frac{1}{m} \sigma^2 和 E(\hat{\mu}) = \mu\)在上面的有效性中已经证明了
所以\(E[\hat{\mu}^2] = \frac{1}{m} \sigma^2 + \mu^2\)

\(E[{x_i}^2] = D(x_i) + E(x_i)^2\)
而\(D(x_i) = \sigma^2 和 E(x_i) = \mu\)在上面的有效性中已经证明了
所以\( \frac{1}{m}E[\sum_{i=1}^mx_i^2] = \frac{1}{m}\sum_{i=1}^m E[x_i^2]= \sigma^2 + \mu^2\)

所以\(E[\hat{\sigma}^2] = \sigma^2 + \mu^2 - (\frac{1}{m} \sigma^2 + \mu^2) =\frac{m-1}{m}\sigma^2\)
所以估计是有偏估计。

所以方差的无偏估计为\(\tilde{\sigma}^2 = \frac{1}{m-1}\sum_{i=1}^m(x_i-\hat{\mu})^2\)

当\(\lim_{m \to \infty}\frac{1}{m}\sum_{i=1}^m(x_i-\hat{\mu})^2 = \frac{1}{m-1}\sum_{i=1}^m(x_i-\hat{\mu})^2\)，也就是说有偏估计是一个渐近无偏估计。

无偏估计不一定是最好的估计！

因子分析FA

因子分析（Factor analysis, FA）

每个变量都可以表示成公共因子的线性函数与特殊因子之和

式中的F1，F2，…，Fm称为公共因子，εi称为Xi的特殊因子。该模型可用矩阵表示为：X = AF+ε
X 表示原始数据，矩阵A称为因子载荷矩阵,F表示公共因子， ε是特殊因子
aij称为因子“载荷”，是第i个变量在第j个因子上的负荷，如果把变量Xi看成m维空间中的一个点，则aij表示它在坐标轴Fj上的投影。
\(X = [X_1,X_2...X_p]^T\)
$A= \begin{bmatrix}
a_{11} & a_{12} & ... & a_{1m} \\
a_{21} & a_{22} & ... & a_{2m} \\
... & ... & ... & ... \\
a_{p1} & a_{p2} & ... & a_{pm} \\
\end{bmatrix}$
\(F = [F_1,F_2...F_m]^T\)
\(\epsilon = [\epsilon_1,\epsilon_2...\epsilon_p]^T\)

主成分分析，是分析维度属性的主要成分表示。
因子分析，是分析属性们的公共部分的表示。
二者均应用于高斯分布的数据，非高斯分布的数据采用独立成分分析ICA算法

独立成分分析ICA

独立成分分析（Independent component analysis, ICA）

X=AS
Y=WX=WAS ， A = inv(W)
ICA(Independent Component Correlation Algorithm)是一种函数，X为n维观测信号矢量，S为独立的m（m<=n)维未知源信号矢量，矩阵A被称为混合矩阵。
ICA的目的就是寻找解混矩阵W（A的逆矩阵），然后对X进行线性变换，得到输出向量Y。

ICA是找出构成信号的相互独立部分(不需要正交)，对应高阶统计量分析。ICA理论认为用来观测的混合数据阵X是由独立元S经过A线性加权获得。
ICA理论的目标就是通过X求得一个分离矩阵W，使得W作用在X上所获得的信号Y是独立源S的最优逼近，

独立成分分析 (ICA) 应用参考(Origin来做ICA分析)

独立成分分析 - 讲解的原理

Independent Component Analysis (ICA)

参考文献

[16-1] 方开泰. 实用多元统计分析. 上海：华东师范大学出版社, 1989.
[16-2] 夏绍玮，杨家本，杨振斌. 系统工程概论. 北京：清华大学出版社，1995.
[16-3] Jolliffe I. Principal component analysis, Sencond Edition. John Wiley & Sons, 2002.
[16-4] Shlens J. A tutorial on principal component analysis. arXiv preprint arXiv: 14016.1100, 2014.
[16-5] Schölkopf B, Smola A, Müller K-R. Kernel principal component analysis. Artificial Neural Networks-ICANN'97. Springer, 1997:583-588.
[16-6] Hardoon D R, Szedmak S, Shawe-Taylor J. Canonical correlation analysis: an overview with application to learning methods. Neural Computation, 2004, 16(12):2639-2664.
[16-7] Candes E J, Li X D, Ma Y, et al. Robust Principal component analysis? Journal of the ACM(JACM), 2011, 58(3):11.

第 17 章 潜在语义分析

我们先介绍下文本信息处理中的一些问题：

1. 一词多义（多义现象）polysemy
   分类时：比如bank 这个单词如果和mortgage, loans, rates 这些单词同时出现时，bank 很可能表示金融机构的意思。可是如果bank 这个单词和lures, casting, fish一起出现，那么很可能表示河岸的意思。

2. 一义多词（同义现象）synonymy
   检索时：比如用户搜索“automobile”，即汽车，传统向量空间模型仅仅会返回包含“automobile”单词的页面，而实际上包含“car”单词的页面也可能是用户所需要的。

LSA能解决同义（语义相似度）问题：发现单词与主题之间的关系，这里主题是汽车；也能解决一定程度的多义问题，同一个单词在不同文档中表示不同话题

潜在语义分析（Latent semantic analysis, LSA）旨在 解决这种方法不能准确表示语义的问题，试图从大量的文本数据中发现潜在的话题，以话题向量表示文本的语义内容，以话题向量空间的度量更准确地表示文本之间的语义相似度。

文本doc集合\(D = \{d_1,d_2,...,d_n\}\)
文本集合中出现的单词word集合\(W = \{w_1,w_2,...,w_m\}\)
单词-文本矩阵(word-document matrix)

权值通常用单词频率-逆文档频率（term frequency–inverse document frequency，TFIDF）表示，定义为：

t为某一个单词（term，word）；d为某一个文档（document）；\(x_{ij} = \text {tf-idf} (w_i,d_j,D)\);D表示文档集合，\(N = |D|\)表示文档总数；

直观上理解：
一个单词在一个文本中出现的频数越高，这个单词在这个文本中的重要度（TF）就越高;
一个单词在整个文档集合中出现的文档数越少，这个单词就越能表示其所在文档的特点，重要度（TDF）就越高；
两种重要度的积，表示综合重要度。
意思就是重要的单词在一个文本中出现的越多越重要，在越少的文本中出现越重要；如：的，可能在每个文档中出现都很多（TF大），并且每个文档都有出现过（TDF小），所以反而不重要了。

相似度(余弦相似度) （Cosine similarity）可以表示两个文本之间的语义相似度，越大越相似。
我们知道训练点积\({\displaystyle \mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\left\|\mathbf {B} \right\|\cos \theta }\),而相似度就是向量之间的夹角\({\displaystyle {\text{similarity}}=\cos(\theta )={\mathbf {A} \cdot \mathbf {B} \over \|\mathbf {A} \|\|\mathbf {B} \|}={\frac {\sum \limits _{i=1}^{n}{A_{i}B_{i}}}{{\sqrt {\sum \limits _{i=1}^{n}{A_{i}^{2}}}}{\sqrt {\sum \limits _{i=1}^{n}{B_{i}^{2}}}}}},}\)

文档用向量表示：\(d_i = x_{.i} = \begin{bmatrix} x_{1i} \\ x_{2i} \\ \vdots \\ x_{mi} \end{bmatrix}\)
那么\(d_i,d_j\)之间的相似度为

这里比较相似度用在了单词向量空间(word vector space model)中，有一个问题就是多义和同义现象，这时我们就可以考虑话题向量空间(topic vector space model):
假设用一个向量表示文档，该向量的每一个分量表示一个话题，其数值为该话题在该文本中的权值，然后比较两个文档相似度（一般话题数远小于单词数）。
潜在语义分析就是构建这样一个话题向量空间的方法。

单词-文本矩阵

那么文档在话题向量空间的表示（话题-文本矩阵）

• 模型：
  
  \[X_{m \times n} \approx T_{m \times k}Y_{k \times n}\]
  
  其中\(X_{m \times n}\)是单词-文本矩阵（就是单词向量空间）；\(T_{m \times k}\)是单词-话题矩阵（就是话题向量空间）；\(Y_{k \times n}\)是话题-文本矩阵，就是我们想要的输出；
  m单词总数，n是文档总数，k是话题总数；
• 策略：
  
  \[minimize \|X - TY\|^2\]
  
  可以看到跟NMF非常像，也可以用TruncatedSVD
• 算法：
  TruncatedSVD:
  
  \[X_{m \times n} \approx X_{rank(k)} = U_{m \times k}\Sigma_{k \times k} V^T_{n \times k}\]
  
  那么话题空间\(T=U_k\)以及本文在话题空间的表示\(Y = \Sigma_kV_k^T\)
  NMF:
  
  \[X \approx WH\]
  
  那么话题空间\(T=W\)以及本文在话题空间的表示\(Y = H\)

参考文献

[17-1] Deerwester S C, Dumais S T, Landauer T K, et al. Indexing by latent semantic analysis. Journal of the Association for Information Science and Technology ,1990, 41: 391-407.
[17-2] Landauer T K. Latent semantic analysis. In: Encyclopedia of Cognitive Science, Wiley, 2006.
[17-3] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization. Nature, 1999, 401(6755):788-791.
[17-4] Lee D D, Seung H S. Algorithms for non-negative matrix factorization. Advances in Neural Information Processing Systems, 2001: 556-562.
[17-5] Xu W, Liu X, Gong Y. Document clustering based on non-negative matrix factorization. Proceedings of the 26th Annual International ACM SIGIR Conference in Research and Development in Information Retrieval, 2003.
[17-6] Wang Q, Xu J, Li H, et al. Regularized latent semantic indexing. Proceedings of the 34th International ACM SIGIR Conference in Research and Development in Information Retrieval, 2011.

第 18 章 概率潜在语义分析

生成模型，用隐变量表示话题

概率潜在语义分析（Probabilistic latent semantic analysis, PLSA）

概率有向图模型：

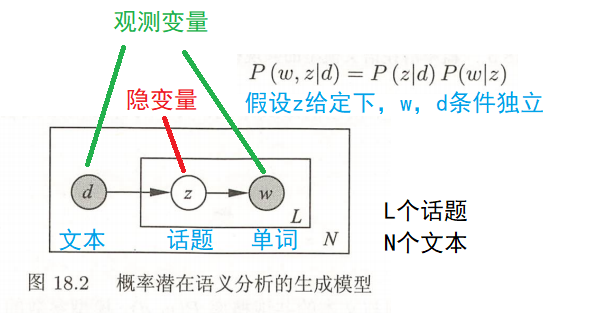
阴影圆表示观测变量，空心圆表示隐变量；箭头表示概率关系；方框表示多次重复，方框内的字母表示重复次数；
文档d是一个观测变量；话题变量z是隐变量(话题的个数是超参数)；单词变量w是一个观测变量；

• 模型：
  单词集合\(W = \{w_1,...,w_M\}\)；
  文本集合\(D=\{d_1,...,d_N\}\)；
  话题集合\(Z=\{z_1,...,z_K\}\)，K是超参数；
  
  \[P(w,d) =P(d)P(w|d) = P(d)\sum_{z} P(w,z|d)=P(d)\sum _{z}P(z|d)P(w|z)\]
  
  \(P(w,z|d) = P(z|d)P(w|z,d) = P(z|d)P(w|z)\)即给定z的情况下w和d相互独立\(w \perp d |z\)
  \(P(w,d)\)是“每个单词-文本对(w,d)”的生成概率
  P(d)表示生成文本d的概率,
  条件概率分布P(z|d)表示文本d生成话题z的概率,
  条件概率分布P(w|z)表示话题z生成单词w 的概率。
  生成（成文本-单词共现数据）步骤：

1. 依据概率分布P(d)，从文本集合中随机选取一个文本d，共生成N个文本；针对每个文本，执行下一步操作
2. 在文本d给定条件下，依据条件概率分布P(z|d)，从话题集合中随机选取一个话题z，共生成L个话题，这里L是文本长度（每个话题生成一个单词，所以生成的文本d的长度是L）
3. 在话题z给定条件下，依据概率分布P(w|z)，从单词集合中随机选取一个单词w

文本-单词共现数据(矩阵T)的生成概率为所有单词-文本对（w，d）的生成概率乘积，

\(n(w,d)\)表示（w，d）出现的次数;
矩阵T的行表示单词，列表示文本，元素表示（w，d）出现的次数，用\(n(w,d)\)表示；
单词-文本对 出现的总次数为N×L

这里假设文本的长度都是等长的，正常情况是第一个文本的长度是L1,...，第N个文本的长度是LN;
正常情况下单词-文本对 出现的总次数为\(\sum_{i=1}^N L_i\)

书中还讲到了等价的共现模型（对称模型）

• 策略：
  

  \[ L =\log P(T) = \log \prod_{i=1}^{M} \prod_{j=1}^{N} {P\left(w_{i}, d_{j}\right)}^{n\left(w_{i}, d_{j}\right) } \\=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log P\left(w_{i}, d_{j}\right) \\ =\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \left[\log P(d)+\log \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right]\]
  
  因为logP(d)对需要求的模型参数无关，我们可以将其省去，于是得到：
  
  \[L =\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \left[ \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right]\]
  
  极大化，得到最优参数
  
  \[\arg \max _{\theta} L(\theta)=\arg \max _{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \left[ \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right) \right]\]

• 算法：
  EM：

1. 现在进行E步，计算Q函数
   

   \[\arg \max _{\theta} L(\theta)=\arg \max _{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\]
   
   其中log右边为关于z的期望：
   
   \[E_z \left[\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] = \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\]
   
   所以：
   
   \[\arg \max _{\theta} L(\theta)=\arg \max _{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log E_z \left[\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right]\]
   
   根据jensen不等式，我们可以得到：
   
   \[\log E_{z}\left[\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] \geq E_{z}\left[\log \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right]\]
   
   得到L(θ)的下界：
   
   \[\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) E_z \left[\log \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] \\ =\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right)\left[\log P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)-\log P\left(z_{k} \mid w_{i}, d_{j}\right)\right]\]
   
   最后，我们将K的累加项拆开，可以得到一项 \(\sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \log P\left(z_{k} \mid w_{i}, d_{j}\right)\) ，这一项在M步中没有作用，可以省去，于是我们可以得到Q函数为：
   
   \[Q=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \log \left[P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right]\]
   
   需要优化的参数为 \(P\left(z_{k} \mid w_{i}, d_{j}\right)，P\left(w_{i} \mid z_{k}\right)， P\left(z_{k} \mid d_{j}\right)\) 这三项，在Q步中，第一项是变量，后两项是常量，于是可以由贝叶斯公式获得：
   
   \[P\left(z_{k} \mid w_{i}, d_{j}\right)=\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{\sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}\]

2. M步
   在M步中，我们需要优化的是\(P\left(w_{i} \mid z_{k}\right)， P\left(z_{k} \mid d_{j}\right)\) 这两项（两项的乘积代表的完全数据，是未知变量），此时 \(P\left(z_{k} \mid w_{i}, d_{j}\right)\)为常量（代表不完全数据，是已知变量），极大化Q函数的M步可以使用拉格朗日乘子法来优化两个参数，即：
   

   \[\max Q \\s.t. \quad \begin{array}{l}\sum_{i=1}^{M} P\left(w_{i} \mid z_{k}\right)=1, \quad k=1,2, \cdots, K \\ \sum_{k=1}^{K} P\left(z_{k} \mid d_{j}\right)=1, \quad j=1,2, \cdots, N\end{array}\]
   
   根据上述约束条件构造拉格朗日函数：
   
   \[\Lambda=Q^{\prime}+\sum_{k=1}^{K} \tau_{k}\left(1-\sum_{i=1}^{M} P\left(w_{i} \mid z_{k}\right)\right)+\sum_{j=1}^{N} \rho_{j}\left(1-\sum_{k=1}^{K} P\left(z_{k} \mid d_{j}\right)\right)\]
   
   分别对两个参数\(P\left(w_{i} \mid z_{k}\right)， P\left(z_{k} \mid d_{j}\right)\)求偏导，并令偏导数为0：
   
   \[\begin{array}{l}\sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)-\tau_{k} P\left(w_{i} \mid z_{k}\right)=0, \quad i=1,2, \cdots, M ; \quad k=1,2, \cdots, K \\ \sum_{i=1}^{M} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)-\rho_{j} P\left(z_{k} \mid d_{j}\right)=0, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K\end{array}\]
   
   求解上面的方程组，就可以得到M步的参数估计：
   
   \[P\left(w_{i} \mid z_{k}\right)=\frac{\sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{\sum_{m=1}^{M} \sum_{j=1}^{N} n\left(w_{m}, d_{j}\right) P\left(z_{k} \mid w_{m}, d_{j}\right)}\]
   
   
   \[P\left(z_{k} \mid d_{j}\right)=\frac{\sum_{i=1}^{M} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{n\left(d_{j}\right)}\]
   
   最后，在E步和M步间不停迭代，直到得到优化后的两个参数
   \(n(d_j) = \sum_{i=1}^M n(w_i,d_j)\)表示文本\(d_j\)中的单词个数，\(n(w_i,d_j)\)表示单词\(w_i\)在文本\(d_j\)中出现的次数。

参考文献

[18-1] Hofmann T. Probabilistic Latent Semantic analysis. Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, 1999: 289-296.
[18-2] Hofmann T. Probabilistic Latent Semantic Indexing. Proceedings of the 22nd Annual International ACM SIGIR Conference in Research and Development in Information Retrieval, 1999.
[18-3] Hofmann T. Unsupervised learning by probabilistic latent semantic analysis. Machine Learning, 2001, 42: 177-196.
[18-4] Ding C, Li T, Peng W. On the equivalence between non-negative matrix factorization and probabilistic latent semantic indexing. Computational Statistics & Data Analysis, 2008, 52(8): 3913-3927.