[TOC]

xx

工具

神经网络绘图工具

http://alexlenail.me/NN-SVG/
非常方便的绘图工具，可视化操作，免费，由麻省理工学院开发
https://github.com/alexlenail/NN-SVG

梯度下降可视化工具

Gradient Descent

梯度下降的可视化解释(Momentum，AdaGrad，RMSProp，Adam)

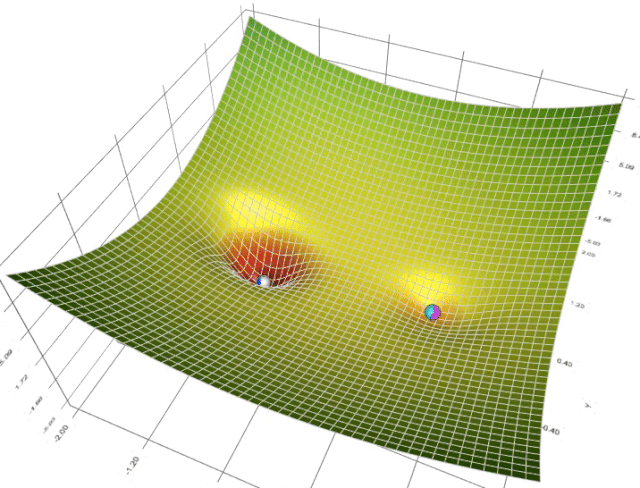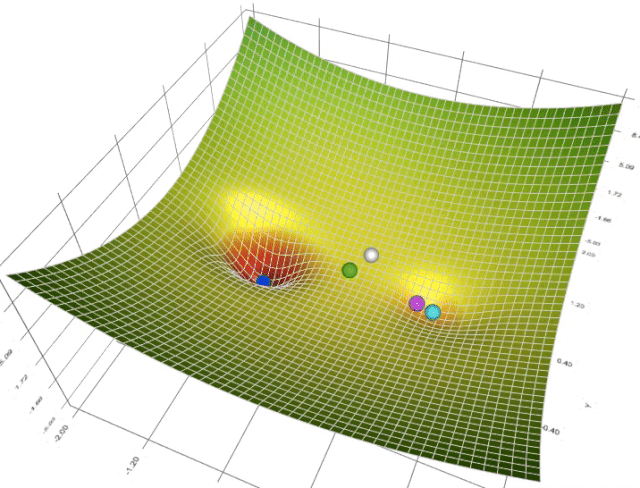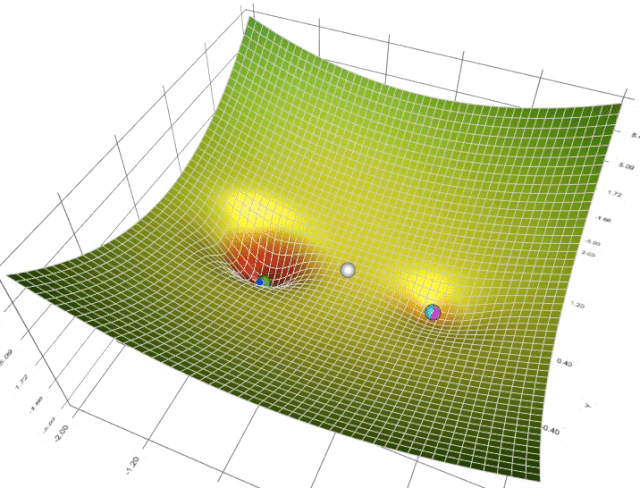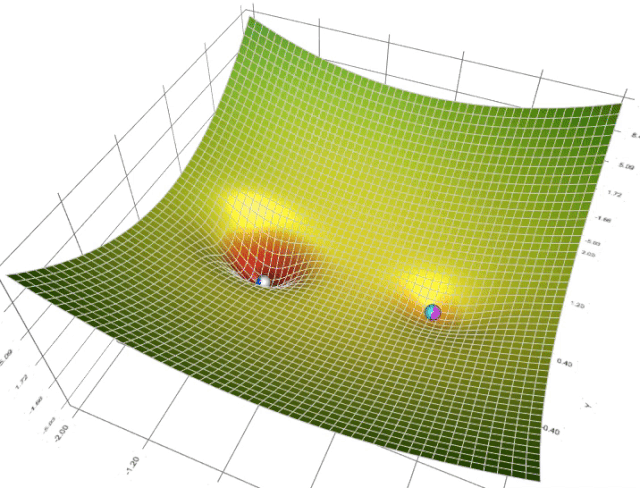
利用动能

机器学习

算法分类

机器学习的算法繁多，其中很多算法是一类算法，而有些算法又是从其他算法中衍生出来的，因此我们可以按照不同的角度将其分类。本文主要通过学习方式和算法类似性这两个角度将机器学习算法进行分类。

学习方式

监督式学习：从给定的训练数据集中学习出一个函数，当新的数据到来时，可以根据这个函数预测结果。监督学习的训练集需要包括输入和输出，也可以说是特征和目标。训练集中的目标是由人标注的。常见的监督式学习算法包括回归分析和统计分类。
非监督式学习：与监督学习相比，训练集没有人为标注的结果。常见的非监督式学习算法有聚类。
半监督式学习：输入数据部分被标识，部分没有被标识，介于监督式学习与非监督式学习之间。常见的半监督式学习算法有支持向量机。
强化学习：在这种学习模式下，输入数据作为对模型的反馈，不像监督模型那样，输入数据仅仅是作为一个检查模型对错的方式，在强化学习下，输入数据直接反馈到模型，模型必须对此立刻作出调整。常见的强化学习算法有时间差学习。

算法类似性

决策树学习：根据数据的属性采用树状结构建立决策模型。决策树模型常常用来解决分类和回归问题。常见的算法包括 CART (Classification And Regression Tree)、ID3、C4.5、随机森林 (Random Forest) 等。
回归算法：试图采用对误差的衡量来探索变量之间的关系的一类算法。常见的回归算法包括最小二乘法 (Least Square)、逻辑回归 (Logistic Regression)、逐步式回归 (Stepwise Regression) 等。
聚类算法：通常按照中心点或者分层的方式对输入数据进行归并。所有的聚类算法都试图找到数据的内在结构，以便按照最大的共同点将数据进行归类。常见的聚类算法包括 K-Means 算法以及期望最大化算法 (Expectation Maximization) 等。
人工神经网络：模拟生物神经网络，是一类模式匹配算法。通常用于解决分类和回归问题。人工神经网络算法包括感知器神经网络 (Perceptron Neural Network) 、反向传递 (Back Propagation) 和深度学习等。
集成算法：用一些相对较弱的学习模型独立地就同样的样本进行训练，然后把结果整合起来进行整体预测。集成算法的主要难点在于究竟集成哪些独立的较弱的学习模型以及如何把学习结果整合起来。这是一类非常强大的算法，同时也非常流行。常见的算法包括 Boosting、Bagging、AdaBoost、随机森林 (Random Forest) 等。

术语库

https://developers.google.com/machine-learning/glossary
https://developers.google.cn/machine-learning/glossary/?hl=zh-cn

SOTA

state of the art 最先进的

课程

https://developers.google.cn/machine-learning/crash-course/ml-intro?hl=zh-cn

总结

损失函数 loss function

机器通过损失函数进行学习。这是一种评估特定算法对给定数据建模程度的方法。如果预测值与实际结果偏离较远，损失函数会得到一个非常大的值。

损失函数是用来计算预测结果和真实结果之间的差，正则化是为了防止模型过拟合，所以在损失函数后面加上一个正则项/惩罚项

训练集、测试集和验证集

静态模型*采用离线训练方式。也就是说，我们只训练模型一次，然后使用训练后的模型一段时间。
动态模型*采用在线训练方式。也就是说，数据会不断进入系统，我们通过不断地更新系统将这些数据整合到模型中。

训练集进行训练模型-> 测试集进行评估模型 -> 选择在测试集上获得最佳效果的模型（可能在不断的超参调优过程中模型会出现过拟合）
训练数据和测试数据应该随机拆分
不要训练测试数据，当测试数据准确率达到100% 请仔细考虑是否正确(过拟合)
数据量少可以考虑使用交叉验证
另一个划分：增加验证数据集（注意区别交叉验证数据集）
训练集进行训练模型-> 验证集进行评估模型 -> 选择在验证集上获得最佳效果的模型 -> 使用测试集确认模型的效果

类别	验证集	测试集
是否被训练到	否	否
作用	纯粹用于调超参数	纯粹为了加试以验证泛化性能
使用次数	多次使用，以不断调参	仅仅一次使用
缺陷	模型在一次次重新手动调参并继续训练后所逼近的验证集，可能只代表一部分非训练集，导致最终训练好的模型泛化性能不够	测试集为了具有泛化代表性，往往数据量比较大，测试一轮要很久，所以往往只取测试集的其中一小部分作为训练过程中的验证集
互相转化	验证集具有足够泛化性（一般来说，如果验证集足够大到包括大部分非训练集时，也等于具有足够泛化性了）	验证集具有足够泛化性时，测试集就没有存在的必要了
类比	校内答辩（如果校内答辩比多校联合答辩还有泛化性（大众）说服力，那么就没有必要再搞个多校联合答辩了）	多校联合公开答辩

训练数据集：训练模型

验证数据集：调整超参数使用的数据集（也就是之前的测试数据集的作用）

将验证数据传给训练好的模型，观察相应的效果：如果效果不好，就重新换参数，重新训练模型…直到找到一组参数，这组参数使得模型针对验证数据来说已经达到最优

测试数据集：作为衡量最终模型性能的数据集(客户验收的数据集-你一般没有)

交叉验证：k-fold cross validation

优化算法

当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解（analytical solution）也叫闭合解（closed-form）。本节使用的线性回归和平方误差刚好属于这个范畴。然而，大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解（numerical solution）。

在求数值解的优化算法中，小批量随机梯度下降（mini-batch stochastic gradient descent）在深度学习中被广泛使用。它的算法很简单：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch）\(\mathcal{B}\)，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

在训练本节讨论的线性回归模型的过程中，模型的每个参数将作如下迭代：

\[ \begin{aligned} w_1 &\leftarrow w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_1} = w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_2} = w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial b} = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned} \]

在上式中，\(|\mathcal{B}|\) 代表每个小批量中的样本个数（批量大小，batch size），\(\eta\) 称作学习率（learning rate）并取正数。需要强调的是，这里的批量大小和学习率的值是人为设定的，并不是通过模型训练学出的，因此叫作超参数（hyperparameter）。我们通常所说的“调参”指的正是调节超参数，例如通过反复试错来找到超参数合适的值。在少数情况下，超参数也可以通过模型训练学出。

为什么权重衰减等价于L2正则化

权重衰减等价于 \(L_2\) 范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。我们先描述\(L_2\)范数正则化，再解释它为何又称权重衰减。

\(L_2\)范数正则化在模型原损失函数基础上添加\(L_2\)范数惩罚项，从而得到训练所需要最小化的函数。\(L_2\)范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以3.1节（线性回归）中的线性回归损失函数

\[ \ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2 \]

为例，其中\(w_1, w_2\)是权重参数，\(b\)是偏差参数，样本\(i\)的输入为\(x_1^{(i)}, x_2^{(i)}\)，标签为\(y^{(i)}\)，样本数为\(n\)。将权重参数用向量\(\boldsymbol{w} = [w_1, w_2]\)表示，带有\(L_2\)范数惩罚项的新损失函数为

\[\ell(w_1, w_2, b) + \frac{\lambda}{2n} \|\boldsymbol{w}\|^2,\]

其中超参数\(\lambda > 0\)。当权重参数均为0时，惩罚项最小。当\(\lambda\)较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当\(\lambda\)设为0时，惩罚项完全不起作用。上式中\(L_2\)范数平方\(\|\boldsymbol{w}\|^2\)展开后得到\(w_1^2 + w_2^2\)。有了\(L_2\)范数惩罚项后，在小批量随机梯度下降中，我们将线性回归一节中权重\(w_1\)和\(w_2\)的迭代方式更改为

\[ \begin{aligned} w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned} \]

可见，\(L_2\)范数正则化令权重\(w_1\)和\(w_2\)先自乘小于1的数，再减去不含惩罚项的梯度。因此，\(L_2\)范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。实际场景中，我们有时也在惩罚项中添加偏差元素的平方和。

梯度更新和泰勒展开公式

一维梯度下降

我们先以简单的一维梯度下降为例，解释梯度下降算法可能降低目标函数值的原因。假设连续可导的函数\(f: \mathbb{R} \rightarrow \mathbb{R}\)的输入和输出都是标量。给定绝对值足够小的数\(\epsilon\)，根据泰勒展开公式，我们得到以下的近似：

\[f(x + \epsilon) \approx f(x) + \epsilon f'(x) .\]

这里\(f'(x)\)是函数\(f\)在\(x\)处的梯度。一维函数的梯度是一个标量，也称导数。

接下来，找到一个常数\(\eta > 0\)，使得\(\left|\eta f'(x)\right|\)足够小，那么可以将\(\epsilon\)替换为\(-\eta f'(x)\)并得到

\[f(x - \eta f'(x)) \approx f(x) - \eta f'(x)^2.\]

如果导数\(f'(x) \neq 0\)，那么\(\eta f'(x)^2>0\)，所以

\[f(x - \eta f'(x)) \lesssim f(x).\]

这意味着，如果通过

\[x \leftarrow x - \eta f'(x)\]

来迭代\(x\)，函数\(f(x)\)的值可能会降低。因此在梯度下降中，我们先选取一个初始值\(x\)和常数\(\eta > 0\)，然后不断通过上式来迭代\(x\)，直到达到停止条件，例如\(f'(x)^2\)的值已足够小或迭代次数已达到某个值。

多维梯度下降

在了解了一维梯度下降之后，我们再考虑一种更广义的情况：目标函数的输入为向量，输出为标量。假设目标函数\(f: \mathbb{R}^d \rightarrow \mathbb{R}\)的输入是一个\(d\)维向量\(\boldsymbol{x} = [x_1, x_2, \ldots, x_d]^\top\)。目标函数\(f(\boldsymbol{x})\)有关\(\boldsymbol{x}\)的梯度是一个由\(d\)个偏导数组成的向量：

\[\nabla_{\boldsymbol{x}} f(\boldsymbol{x}) = \bigg[\frac{\partial f(\boldsymbol{x})}{\partial x_1}, \frac{\partial f(\boldsymbol{x})}{\partial x_2}, \ldots, \frac{\partial f(\boldsymbol{x})}{\partial x_d}\bigg]^\top.\]

为表示简洁，我们用\(\nabla f(\boldsymbol{x})\)代替\(\nabla_{\boldsymbol{x}} f(\boldsymbol{x})\)。梯度中每个偏导数元素\(\partial f(\boldsymbol{x})/\partial x_i\)代表着\(f\)在\(\boldsymbol{x}\)有关输入\(x_i\)的变化率。为了测量\(f\)沿着单位向量\(\boldsymbol{u}\)（即\(\|\boldsymbol{u}\|=1\)）方向上的变化率，在多元微积分中，我们定义\(f\)在\(\boldsymbol{x}\)上沿着\(\boldsymbol{u}\)方向的方向导数为

\[\text{D}_{\boldsymbol{u}} f(\boldsymbol{x}) = \lim_{h \rightarrow 0} \frac{f(\boldsymbol{x} + h \boldsymbol{u}) - f(\boldsymbol{x})}{h}.\]

依据方向导数性质[1，14.6节定理三]，以上方向导数可以改写为

\[\text{D}_{\boldsymbol{u}} f(\boldsymbol{x}) = \nabla f(\boldsymbol{x}) \cdot \boldsymbol{u}.\]

方向导数\(\text{D}_{\boldsymbol{u}} f(\boldsymbol{x})\)给出了\(f\)在\(\boldsymbol{x}\)上沿着所有可能方向的变化率。为了最小化\(f\)，我们希望找到\(f\)能被降低最快的方向。因此，我们可以通过单位向量\(\boldsymbol{u}\)来最小化方向导数\(\text{D}_{\boldsymbol{u}} f(\boldsymbol{x})\)。

由于\(\text{D}_{\boldsymbol{u}} f(\boldsymbol{x}) = \|\nabla f(\boldsymbol{x})\| \cdot \|\boldsymbol{u}\| \cdot \text{cos} (\theta) = \|\nabla f(\boldsymbol{x})\| \cdot \text{cos} (\theta)\)，
其中\(\theta\)为梯度\(\nabla f(\boldsymbol{x})\)和单位向量\(\boldsymbol{u}\)之间的夹角，当\(\theta = \pi\)时，\(\text{cos}(\theta)\)取得最小值\(-1\)。因此，当\(\boldsymbol{u}\)在梯度方向\(\nabla f(\boldsymbol{x})\)的相反方向时，方向导数\(\text{D}_{\boldsymbol{u}} f(\boldsymbol{x})\)被最小化。因此，我们可能通过梯度下降算法来不断降低目标函数\(f\)的值：

\[\boldsymbol{x} \leftarrow \boldsymbol{x} - \eta \nabla f(\boldsymbol{x}).\]

同样，其中\(\eta\)（取正数）称作学习率。

下面我们构造一个输入为二维向量\(\boldsymbol{x} = [x_1, x_2]^\top\)和输出为标量的目标函数\(f(\boldsymbol{x})=x_1^2+2x_2^2\)。那么，梯度\(\nabla f(\boldsymbol{x}) = [2x_1, 4x_2]^\top\)。我们将观察梯度下降从初始位置\([-5,-2]\)开始对自变量\(\boldsymbol{x}\)的迭代轨迹。我们先定义两个辅助函数，第一个函数使用给定的自变量更新函数，从初始位置\([-5,-2]\)开始迭代自变量\(\boldsymbol{x}\)共20次，第二个函数对自变量\(\boldsymbol{x}\)的迭代轨迹进行可视化。

参考

梯度下降 Gradient Descent

在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。

当前的点x1 - 学习速率 * 导数 = 新的点x2

https://ruder.io/optimizing-gradient-descent/index.html

梯度下降法和其他无约束优化算法的比较

在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。
相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

优化器

https://ruder.io/optimizing-gradient-descent/index.html
SGD
Momentum
NAG
Adagrad
Adadelta
Rmsprop

# optimizer：优化器； learning_rate 学习速率(步长)
# SGD->Stochastic随机的 Gradient Descent 梯度下降
optimizer = optimizers.SGD(learning_rate=0.001, momentum=0.9)


# momentum 动力，

# 如何选择优化算法?
#
# 如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam。
# RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。
# Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，
# 随着梯度变的稀疏，Adam 比 RMSprop 效果会好。
# 整体来讲，Adam 是最好的选择。
# 很多论文里都会用 SGD，没有 momentum 等。SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点，这时就需要momentum参数了，一般0.9。

# 深度学习——优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）
# https://www.cnblogs.com/guoyaohua/p/8542554.html

特征

特征组合 (feature cross)

通过将单独的特征进行组合（求笛卡尔积）而形成的合成特征。特征组合有助于表达非线性关系。

[A X B]：将两个特征的值相乘形成的特征组合。
[A x B x C x D x E]：将五个特征的值相乘形成的特征组合。
[A x A]：对单个特征的值求平方形成的特征组合。

过拟合和欠拟合

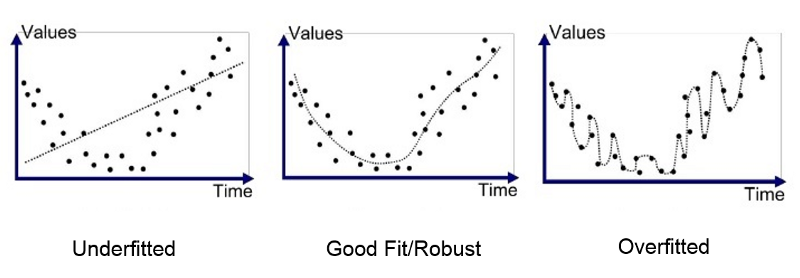
如果减轻过拟合 - 正则化和 Dropout 和Early stopping

如果知道过拟合 - 验证和测试

动量 Momentum

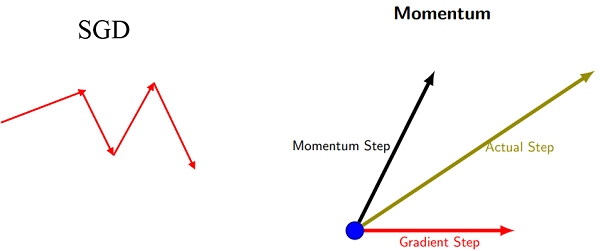
理想情况：（常见的的值0.9）

改变实际梯度下降的方向
当正常的梯度下降时到达局部最小解时，由于动力的惯性可以找到全局最小解

学习速率

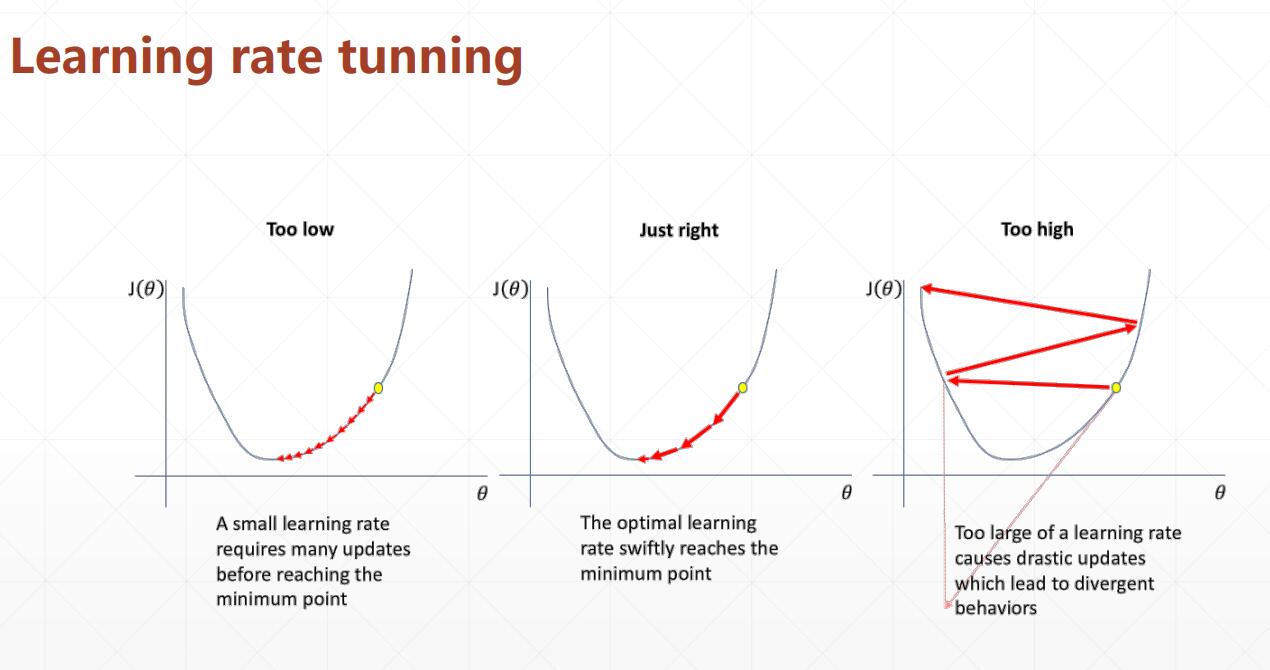
Learning rate decay 衰弱

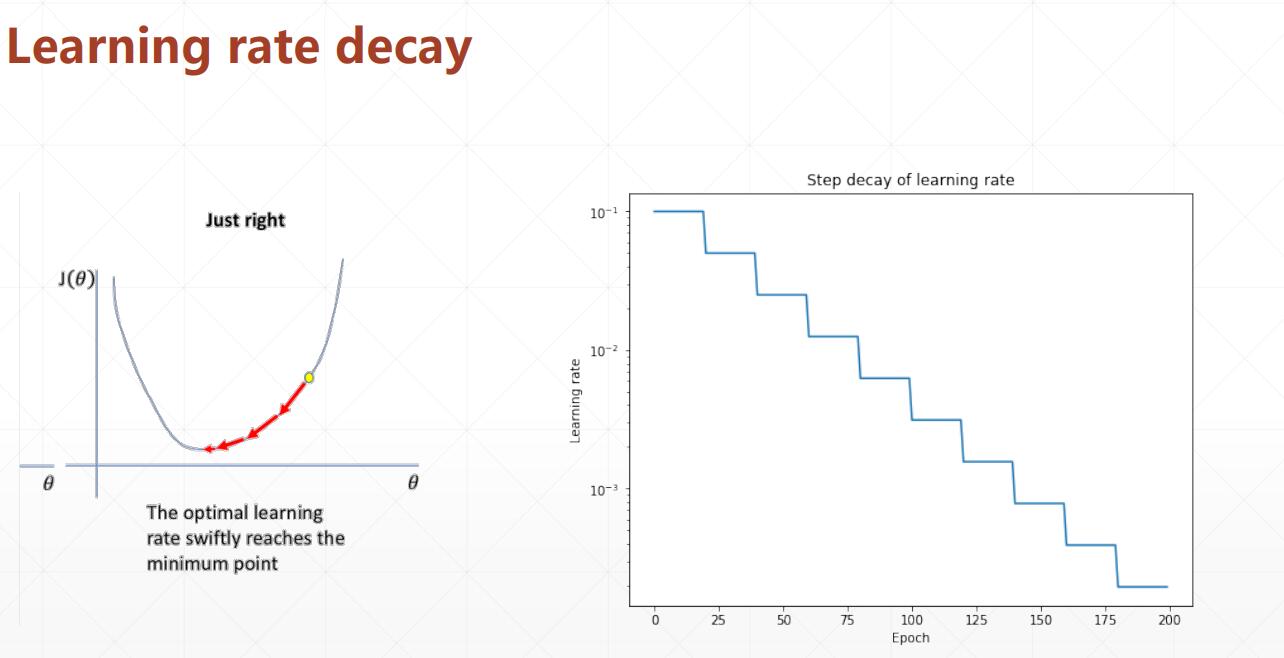
如何做

Dropout

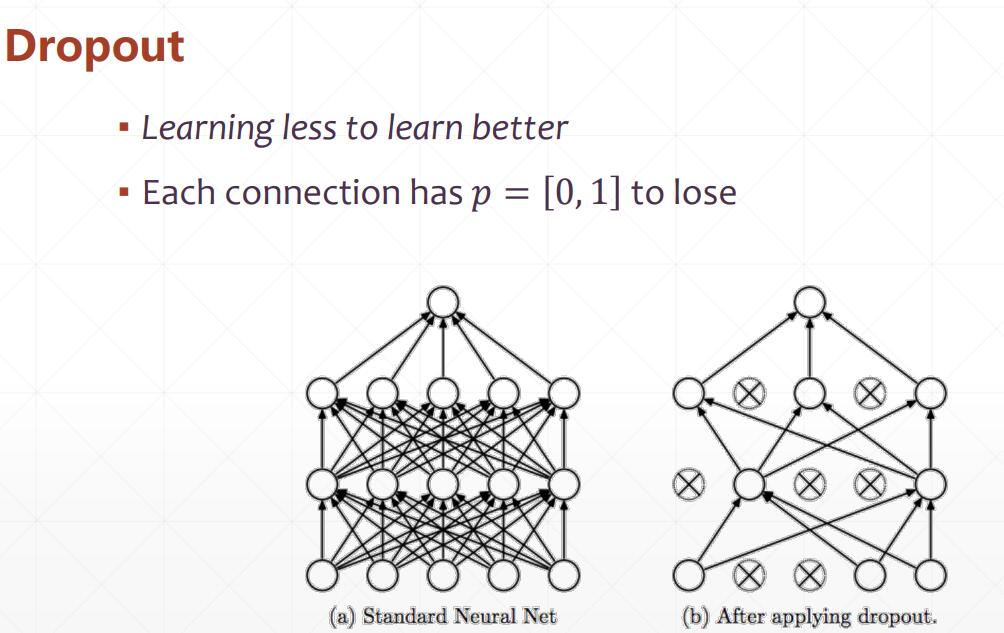
BatchNorm 归一化

减少梯度消失，加快了收敛过程。

起到类似dropout一样的正则化能力，一定程度上防止过拟合。

放宽了一定的调参要求。

可以替代LRN。使用：Tensorflow 提供了函数 tf.nn.lrn()来完成这个操作。

Early stopping

当在验证集上面开始下降的时候中断训练，一种方式使用TensorFlow去实现，是间隔的比如每50 steps，在验证集上去评估模型，然后保存一下快照如果输出性能优于前面的快照，记住最后一次保存快照时候迭代的steps的数量，当到达step的limit次数的时候，restore最后一次胜出的快照。
尽管early stopping实际工作做不错，你还是可以得到更好的性能当结合其他正则化技术一起的话

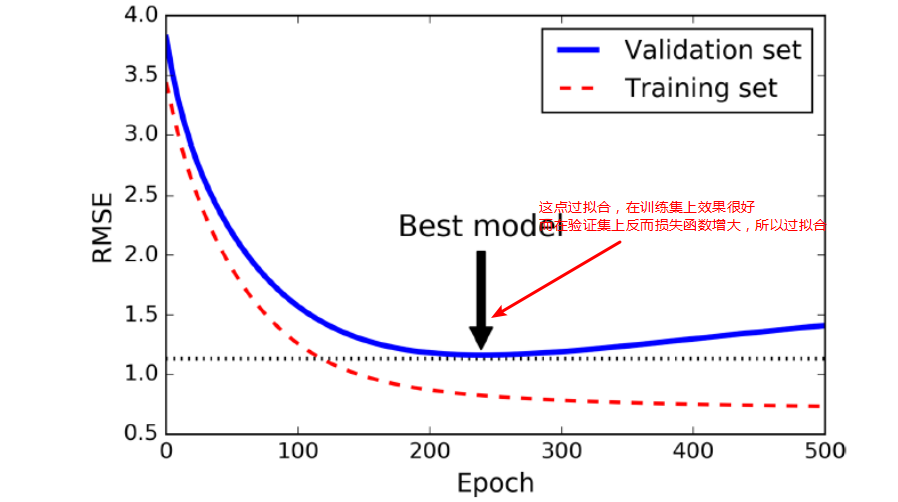
每次训练一（N）个epoch就验证下,判断是否需要保存

正则化

排除噪点，增加泛化能力

lambda（又称为正则化率）就是惩罚因子

注意：将 lambda 设为 0 可彻底取消正则化。在这种情况下，训练的唯一目的将是最小化损失，而这样做会使过拟合的风险达到最高。

L1正则化与L2正则化的理解

L1正则化

稀疏性正则化 (Regularization for Sparsity)：L₁ 正则化
和 L2 不同，L1 鼓励稀疏性

稀疏矢量通常包含许多维度。创建特征组合会导致包含更多维度。由于使用此类高维度特征矢量，因此模型可能会非常庞大，并且需要大量的 RAM。

在高维度稀疏矢量中，最好尽可能使权重正好降至 0。正好为 0 的权重基本上会使相应特征从模型中移除。将特征设为 0 可节省 RAM 空间，且可以减少模型中的噪点。

L1 正则化可能会使信息丰富的特征的权重正好为 0.0。
L1 正则化会使大多数信息缺乏的权重正好为 0.0。
L1 正则化往往会减少特征的数量。也就是说，L1 正则化常常会减小模型的大小。

L2 正则化可以使权重变小，但是并不能使它们正好为 0.0。

L2 和 L1 采用不同的方式降低权重：

L2 会降低权重^2^。
L1 会降低 |权重|。

因此，L2 和 L1 具有不同的导数：

L2 的导数为 2 * 权重。
L1 的导数为 k（一个常数，其值与权重无关）。

准确率、精确率、召回率

精确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。

召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。

demo1
假设我们手上有60个正样本，40个负样本，我们要找出所有的正样本，系统查找出50个，其中只有40个是真正的正样本，计算上述各指标。
TP: 将正类预测为正类数 40(系统查找出40个是真正的正样本)
FN: 将正类预测为负类数 20(60个正样本 - 系统查找出40个是真正的正样本)
FP: 将负类预测为正类数 10(系统查找出50个 - 系统查找出40个是真正的正样本)
TN: 将负类预测为负类数 30(系统查找出50个正样本，那么就是预测了50个负样本，但是50个认为的负样本中实际上有20个正样本，所以30=50-20)

准确率(accuracy)(ACC) = 预测对的/所有 = (TP+TN)/(TP+FN+FP+TN) = 70%

精确率(precision)(PPV) = TP/(TP+FP) = 80%

召回率(recall) = TP/(TP+FN) = 2/3

灵敏度（Sensitivity）（TPR）：就是召回率（Recall）召回率 = 提取出的正确信息条数 / 样本中的信息条数。通俗地说，就是所有准确的条目有多少被检索出来了

真正例率 (TPR) 是召回率的同义词 = TP/(TP+FN)

假正例率 (FPR) = FP/(FP+TN)

特异度(TNR) Specificity = TN/(TN+FP)

以上都是二级指标

三级指标 F1 Score = 2PR/(P+R)
其中，P代表Precision，R代表Recall。
F1-Score指标综合了Precision与Recall的产出的结果。
F1-Score的取值范围从0到1的，1代表模型的输出最好，0代表模型的输出结果最差

1）TP就是【True P】;FP就是【False P】。都是站在预测的角度来描述的。
（2）P代表的是Positive【正类】; N表示的是Negative【负类】

Positive代表原始类别，而Negative代表其他所有的类别

FN：False Negative,被判定为负样本，但事实上是正样本。
FP：False Positive,被判定为正样本，但事实上是负样本。
TN：True Negative,被判定为负样本，事实上也是负样本。
TP：True Positive,被判定为正样本，事实上也是正样本。

demo2
分类阈值（也称为判定阈值）。如果值高于该阈值，则表示“垃圾邮件”；如果值低于该阈值，则表示“非垃圾邮件”。人们往往会认为分类阈值应始终为 0.5，但阈值取决于具体问题，因此您必须对其进行调整。

让我们以一种将电子邮件分为“垃圾邮件”或“非垃圾邮件”这两种类别的分类模型为例。
如果提高分类阈值，
精确率可能会提高:一般来说，提高分类阈值会减少假正例，从而提高精确率。
召回率始终下降或保持不变:提高分类阈值会导致真正例的数量减少或保持不变，而且会导致假负例的数量增加或保持不变。因此，召回率会保持不变或下降。

注意：“调整”逻辑回归的阈值不同于调整学习速率等超参数。在选择阈值时，需要评估您将因犯错而承担多大的后果。例如，将非垃圾邮件误标记为垃圾邮件会非常糟糕。不过，虽然将垃圾邮件误标记为非垃圾邮件会令人不快，但应该不会让您丢掉工作。反之将非垃圾邮件标记为垃圾邮件，那么你可以回家了。

准确率 = (TP+TN)/(TP+FN+FP+TN) = (1+90)/(1+90+1+8) = 0.91
精确率 = TP/(TP+FP) = 1/(1+1) = 0.5 ，也就是说，该模型在预测恶性肿瘤方面的正确率是 50%。
召回率 = TP/(TP+FN) = 1/(1+8) = 0.11，也就是说，该模型能够正确识别出所有恶性肿瘤的百分比是 11%。

以上数据说明：

当您使用分类不平衡的数据集（比如正类别标签和负类别标签的数量之间存在明显差异）时，单单准确率一项并不能反映全面情况。
判断模型的好坏需要通过准确率和召回率两个指标来判断

demo4

在 roulette 游戏中，一只球会落在旋转轮上，并且最终落入 38 个槽的其中一个内。某个机器学习模型可以使用视觉特征（球的旋转方式、球落下时旋转轮所在的位置、球在旋转轮上方的高度）预测球会落入哪个槽中，准确率为 4%。
这个机器学习模型做出的预测比碰运气要好得多；随机猜测的正确率为 1/38，即准确率为 2.6%。尽管该模型的准确率“只有”4%，但成功预测获得的好处远远大于预测失败的损失。

分类 (Classification)：检查您的理解情况（ROC 和 AUC）

激活函数，梯度消失与梯度爆炸

如果每层因子相乘的结果不断减小，产生梯度消失，会造成网络的前层网络的权重的梯度很小，这些w很可能得不到更新；而如果相乘的结果越来越大，则产生梯度爆炸。

非线性变化，例如激活函数

激活函数（例如 ReLU 或 S 型函数），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。

在下图所示的模型中，在隐藏层 1 中的各个节点的值传递到下一层进行加权求和之前，我们采用一个非线性函数对其进行了转换。这种非线性函数称为激活函数。

线性回归：out = w*x + b
逻辑(非线性)回归：需要添加非线性函数（激活函数）f;使得 out = f(w*x + b) ：比如f=relu

hide1(隐藏层) = relu(w1@x + b1)
hide2(隐藏层) = relu(w2@hide1 + b2)
out = relu(w3@hide2 + b3)

为什么deep ？hide 非常多

x输入如果是矩阵，那么w和b 也是矩阵，这样就可以实现降维：

激活函数的由来

1959年，生物科学家研究青蛙神经元的时候发现，青蛙的神经元有多个输入，神经元中间有一个多输入加权后的相应，当该响应小于阈值时没有输出，当该响应大于阈值是会有一个固定的输出。当时的计算机科学家借鉴于此发明了一个计算机模型，如下图：

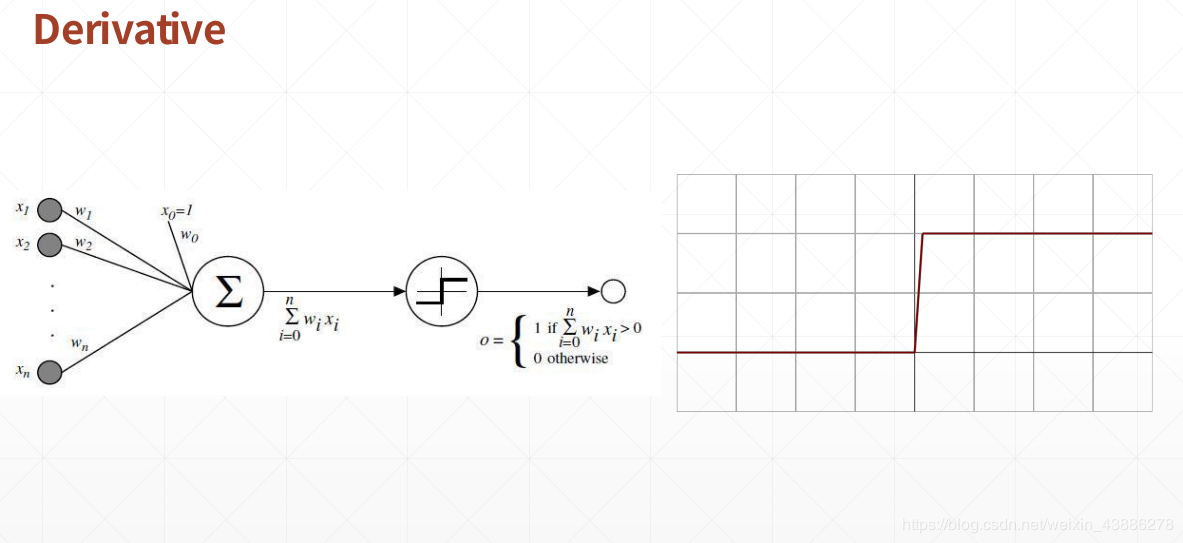
假设z为输入经过加权后的值，z小于阈值输出0，z大于阈值输出1。（阶梯函数）
为了解决阶梯函数在阶梯处不可导的缺点，计算机学家们引入了sigmoid函数

常见的激活函数

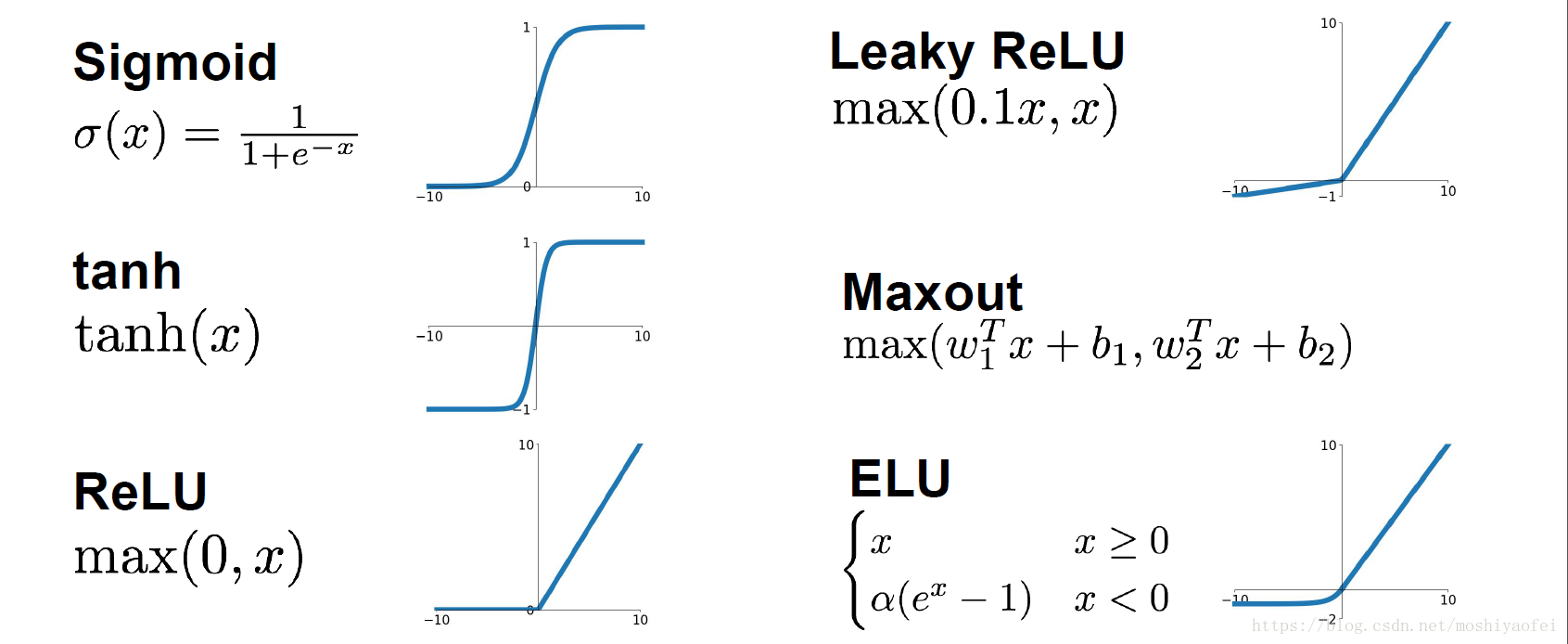
使用场景：
1、在输出层，一般会使用sigmoid函数，因为一般期望的输出结果概率在0~1之间，如二分类，sigmoid可作为输出层的激活函数
2、在隐藏层，tanh函数优于sigmoid函数。因为其取值范围介于-1 ~ 1之间，有类似数据中心化的效果。
3、但实际应用中，tanh和sigmoid会在端值趋于饱和，造成训练速度减慢，故一般的深层网络的激活函数默认大多采用relu函数，也可以前面几层使用relu函数，后面几层使用sigmoid函数。

Relu Rectified Linear Unit 调整线性单元

max(0,x)

x<0时，输出为0, 否则输出x
存在的问题：

x<0时，输出为0，可能导致某些神经元死亡
不是zero-center
无负值

tf.nn.relu

ReLU在自变量大于0时导数为1,小于0时导数为0,因此可以解决梯度爆炸问题.

ReLU 梯度：<0 梯度0 >0 梯度1

S 型激活函数

S 型激活函数将加权和转换为介于 0 和 1 之间的值

存在的问题：
（1）梯度消失

（2）sigmod函数的输出不是以0为中心的

（3）exp()计算的代价大

Sigmoid

f(x) = 1/(1+e^-x^)

x = 0 ,f(x) =y=0.5
x > 0,f(x) =y>0.5 & <1
x <> 0,f(x) =y<0.5 & >0

一般 x=5 基本上f(x) =y = 0.9933
一般 x=-5 基本上f(x) =y = 0.0067
tf.sigmoid

tanh

(-1,1)
tanh(x) = sinh(x)/cosh(x) = (e^x^ - e^-x^)/(e^x^ + e^-x^)

tanh(0) = 0
-5 = -0.9999
-2.5 = -0.9866
2.5 = 0.9866
3 = 0.995
5 = 0.9999

梯度消失

较低层（更接近输入）的梯度可能会变得非常小。在深度网络中，计算这些梯度时，可能涉及许多小项的乘积。

当较低层的梯度逐渐消失到 0 时，这些层的训练速度会非常缓慢，甚至不再训练。

ReLU 激活函数有助于防止梯度消失。

梯度爆炸

如果网络中的权重过大，则较低层的梯度会涉及许多大项的乘积。在这种情况下，梯度就会爆炸：梯度过大导致难以收敛。

批标准化可以降低学习速率，因而有助于防止梯度爆炸。

ReLU 单元消失

一旦 ReLU 单元的加权和低于 0，ReLU 单元就可能会停滞。它会输出对网络输出没有任何贡献的 0 激活，而梯度在反向传播算法期间将无法再从中流过。由于梯度的来源被切断，ReLU 的输入可能无法作出足够的改变来使加权和恢复到 0 以上。

降低学习速率有助于防止 ReLU 单元消失。

Loss

MSE 均方差

Deep Learning

深度学习是机器学习的一个子领域，研究受大脑结构和功能启发的算法。这些算法被称为人工智能网络，它由层层排列的函数（神经元）组成，它们将信号传递给其他神经元。这些信号是输入到网络中的数据的产物，从一层传递到另一层，并对网络进行缓慢的“调整”，实际上是在调整每个连接的突触强度（权重）。通过数据集中提取特征并识别交叉样本的趋势，网络最终学会做出预测。

CNN

卷积神经网络的端到端结构

一般图像处理使用2DConvolution层

卷积神经网络简介

卷积神经网络

卷积核

DL 中的卷积核（就像一个w参数）是自己学到的

CV常见的卷积核

sharpen 锐化

0	-1	0
-1	5	-1
0	-1	0

Blur 模糊
Edge Detect 边缘检测

0	1	0
1	-4	1
0	1	0

3DConvolution层

三维卷积对三维的输入进行滑动窗卷积，当使用该层作为第一层时，应提供input_shape参数。
例如input_shape = (3,10,128,128)代表对10帧128*128的彩色RGB图像进行卷积。

# demo01
#160*100*22
model.add(Convolution3D(
    10,
    kernel_dim1=9, # depth
    kernel_dim2=9, # rows
    kernel_dim3=9, # cols
    input_shape=(3,160,100,22),
    activation='relu'
))
#now 152*92*14

# demo02

#34*19*8
model.add(Convolution3D(
    50,
    kernel_dim1=5, # depth
    kernel_dim2=9, # rows
    kernel_dim3=8, # cols
    activation='relu'
))
#now 26*12*4

softmax

适合多分类问题
给定一些数字，Softmax函数就能将任意数字转化为概率

比如，我们选定数字 -1、0、3和5。

首先，我们需要计算e的指定数字次方，然后将其所有结果相加，当作分母。
denominator = e^-1^ + e^0^ + e^3^ + e^5^ = 169.87

最后，e的指定数字次方的值就作为分子，由此计算可能性。

金字塔 -> 5没有3的两倍 -> 概率却是它的8倍，哪怕你比别人大一点，你的收益(概率)却比别人大很多

https://victorzhou.com/blog/softmax/

待学习迁移学习 Transfer Learning 元学习 meta-learning Few-shot learning（少样本学习） learning to learn，就是学会学习

待学习 Artificial Neural Networks (ANN) RNN CNN

ann可视化：https://github.com/Prodicode/ann-visualizer

待学习 seq2seq BERT YOLOv5 对决 Faster RCNN

目前，基于深度学习(deep learning)的目标检测技术效果是最好的，这些技术模型可以分成三类：

基于Region Proposal（候选区域）的算法如：R-CNN系列，包括R-CNN，Fast R-CNN，以及Faster R-CNN
Single Shot Detector (SSD)
You Only Look Once (YOLO)系列，其中YOLOv3是今天的主角

目标检测算法主要分为两类：
一类是基于Region Proposal（候选区域）的算法，如R-CNN系算法（R-CNN，Fast R-CNN, Faster R-CNN），它们是two-stage（两步法）的，需要先使用Selective search或者CNN网络（RPN）产生Region Proposal，然后再在Region Proposal上做分类与回归。
而另一类是Yolo，SSD这类one-stage算法（一步法），其仅仅使用一个CNN网络直接预测不同目标的类别与位置。
第一类方法是准确度高一些，但是速度慢，而第二类算法是速度快，但是准确性要低一些。

https://pjreddie.com/darknet/yolo/

NLP

GRU，LSTM，XLNet，BERT

最强大的语言模型GPT-3（也有图片模型GPT-3）

GPT 模型是 OpenAI 在 2018 年提出的一种新的 ELMo 算法模型，该模型在预训练模型的基础上，只需要做一些微调即可直接迁移到各种 NLP 任务中，因此具有很强的业务迁移能力。

互联网原子弹，人工智能界的卡丽熙，算力吞噬者，黄仁勋的新 KPI ，下岗工人制造机，幼年期的天网 —— 最先进的 AI 语言模型 GPT-3。
GPT-3开启“天网元年”。GPT-3是来自黑暗大陆的模型。

在语言方面，依赖于单词预测的无监督学习算法（例如GPT-3和BERT）非常成功

另外两个主要的技术趋势会让程序员倍感不安：无代码编程和AutoML.

无代码编程指的是一种可视化工具，任何人都可以通过这种可视化工具轻松地构建新产品，无论是网站、设计、数据分析还是模型都没问题。
AutoML，即自动机器学习，它大大缩短了AI投入生产的时间。

GPT-3将再一次掀起无代码编程和AutoML工具的热潮。

你不仅可以指导GPT-3编写代码，而且还可以指导它编写诗歌、音乐、社交媒体评论或任何其他文本。

GPT可以编写代码(比如SQL，其它任何语言)，可以编写任何东西，而且它还可以生成图像。
同一个模型体系结构不仅可以用于处理文本，还可在像素序上进行训练，从而生成新的图像。实际上，GPT的表现出人意料，甚至可与顶级的CNN媲美。

OpenAI 曾于 2019 年初发布 GPT-2，这一基于 Transformer 的大型语言模型共包含 15 亿参数、在一个 800 万网页数据集上训练而成，这在当时就已经引起了不小的轰动。整个 2019 年，GPT-2 都是 NLP 界最耀眼的明星之一，与 BERT、Transformer XL、XLNet 等大型自然语言处理模型轮番在各大自然语言处理任务排行榜上刷新最佳纪录。而 GPT-2 得益于其稳定、优异的性能在业界独领风骚。

而 GPT-3 的参数量足足是 GPT-2 的 116 倍（GPT-3，1750 亿参数，45TB 训练数据），实现了对整个 2019 年的所有大型自然语言处理模型的降维打击。

在 NLP 领域中，通常采用 ELMo 算法的思想，即通过在大量的语料上预训练语言模型，然后再将预训练好的模型迁移到具体的下游NLP任务，从而提高模型的能力。GPT 模型是 OpenAI 在 2018 年提出的一种新的 ELMo 算法模型，该模型在预训练模型的基础上，只需要做一些微调即可直接迁移到各种 NLP 任务中，因此具有很强的业务迁移能力。

GPT 模型主要包含两个阶段。第一个阶段，先利用大量未标注的语料预训练一个语言模型，接着，在第二个阶段对预训练好的语言模型进行微改，将其迁移到各种有监督的 NLP 任务，并对参数进行 fine-tuning。

在 GPT-3 之前，最大的 AI 语言模型是微软在今年（2020） 2 月推出的 Turing NLG，当时拥有 170 亿参数的 Turing NLG 已经标榜是第二名 Megatron-LM 的两倍。没错，仅短短 5 个月的时间，GPT-3 就将头号玩家的参数提高了 10 倍！

微软给 OpenAI 提供的这台超级计算机是一个统一的系统，该系统拥有超过 285000 个 CPU 核心，10000 个 GPU 和每秒 400G 的网络，是一台排名全球前 5 的超级计算机。
有专业人士推测过，训练一个GPT-3模型需要“355个GPU年”（一块GPU运行355年的运算量），光是训练费用就高达460万美元。（光训练好的model有700GB - GPT-2 才6GB）
700GB = 1750亿*4byte / 1024 / 1024 /1024 = 652GB

(有BUG也不敢重新训练~~太贵了)

最后引用神经网络之父、图灵奖获得者 Geoffrey Hinton 早前对 GPT-3 的一番评论：

“ 鉴于 GPT-3 在未来的惊人前景，可以得出结论：生命、宇宙和万物的答案，就只是 4.398 万亿个参数而已。”

参考链接：

https://blogs.microsoft.com/ai/openai-azure-supercomputer/
https://jalammar.github.io/how-gpt3-works-visualizations-animations/
https://www.reddit.com/r/MachineLearning/comments/hymqof/d_gpt3_and_a_typology_of_hype_by_delip_rao/
https://www.datanami.com/2020/07/21/openais-gpt-3-language-generator-is-impressive-but-dont-hold-your-breath-for-skynet/

GPT-3应用案例：
https://gpt3examples.com/

GPT-3沙箱：
https://github.com/shreyashankar/gpt3-sandbox

OpenAI API开发者工具包：
https://www.notion.so/API-Developer-Toolkit-49595ed6ffcd413e93ebff10d7e70fe7

awesome-gpt3:
https://github.com/elyase/awesome-gpt3

https://lambdalabs.com/blog/gpt-3/

one-hot

手写数字问题：[28 , 28, 1]的图片矩阵 - 打平第二行28 放到第一行的右边，总共变成一维[28*28 = 748]

输出（prediction）：

dog = 0, cat =1 ,fish = 2 ...
one-hot 编码
dog =[1,0,0,...]
cat = [0,1,0,0,..]
fish = [0,0,1,0,..]

一般在输出结果之前的数据格式为[dog=0.9,cat=0.1] 它们的概率之和为1，我们取最大的

张量的数据形式

tensor:张量
dim：代表张量的维度。
constant:常量

标量(scalar)：数据单独的一个数，零维张量，其形状如：1.1 ,dim=0 ,shape=()

向量(vector) ：一维数组，一维张量，其形状如：[1.1,2.2,3.3] ,dim=1 ,shape=(3,)

矩阵(matrix)：二维数组，二维张量，其形状如：shape=(3,3)

多维数组(n-d array)：多维数组，多维张量，其形状如：shape=(1,3,3)

shape：shape描述的是矩阵的形状, 即张量的shape。从前往后对应由外向内的维度。

size：size描述的是元素的个数。

dim：代表张量的维度。

[[1],[2],[3]] 这个张量的shape为（3,1）
[[[1,2],[3,4]],[[5,6],[7,8]],[[9,10],[11,12]]]这个张量的shape为（3,2,2）,
[1,2,3,4]这个张量的shape为（4，）

1-5维的张量应用场景

dim = 0 （0阶张量）, 标量(scalar), shape = () ,5 比如np.array(5)
loss 和 accuracy

dim = 1 ,向量(vector), shape = (2,) , [1,2]

net.bias

# W @ x + b
net = layers.Dense(10)
net.build((4, 8))

net.kernel # w,shape = (8,10)
net.bias # b, shape =(10,)

dim = 2 ,矩阵(matrix)，shape = (2,2)，[[1,2],[3,4]]
一般 input x :[b, vec_dim] (一张图片[1,784]，多张图片[b,784])
weight : [input_dim, output_dim]

dim = 3, tensor张量, [25000, 80, 200]
比如NLP中
x:[b,seq_len, word_dim]

将每个单词转换为word_dim = 200长度的
那么seq_len = 单词个数
b= 句子个数

对单词embedding

dim = 4, tensor张量, [60000, 28, 28, 3]
比如图片：[b,h,w,3]
b个图片个数

dim = 5 ,tensor张量
可以看做对dim=4的批量
[task_b,b,h,w,3] 有task_b个任务，每个任务[b,h,w,3]

Table of Contents

xx

工具